高中数学选择题

一直线运动的物体，从时间t到t+△t时，物体的位移为△s，那么为（ ）

A．从时间t到t+△t时，物体的平均速度

B．时间t时该物体的瞬时速度

C．当时间为△t时该物体的速度

D．从时间t到t+△t时位移的平均变化率

f（x）=sinx在x=0和x=两处的瞬时变化率为k₁和k₂，则k₁+k₂为（ ）

A．﹣1

B．1

C．0

D．无法确定

设f（x）在x处可导，则等于（ ）

A．2f′（x）

B．f′（x）

C．f′（x）

D．4f′（x）

有人从“若a＜b，则2a＜＜2b”中找到灵感引入一个新概念，设F（x）=x²，f（x）=2x，于是有f（a）＜＜f（b），此时称F（x）为甲函数，f（x）为乙函数，下面命题正确的是（ ）

A．若f（x）=3x^2+2x则F（x）=x^3+x^2+C，C为常数

B．若f（x）=cosx，则F（x）=sinx+C，C为常数

C．若f（x）=x^2+1，则F（x）为奇函数

D．若f（x）=e^x，则F（2）＜F（3）＜F（5）

路灯距离地面8m，一个身高为1.6m的人以84m/min的速度从路灯在地面上的射影点O沿某直线离开路灯，那么人影长度的变化速率为（ ）

A．m/s

B．m/s

C．m/s

D．m/s

某汽车启动阶段的位移函数为s（t）=2t³﹣5t²，则汽车在t=2时的瞬时速度为（ ）

A．10

B．14

C．4

D．6

已知某质点的位移s与移动时间t满足s=t²•e^t﹣2，则质点在t=2的瞬时速度是（ ）

A．4

B．6

C．8

D．16

质点运动规律s=t²+3，则在时间（3，3+△t）中，相应的平均速度是（ ）

A．6+△t

B．6+△t+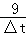

C．3+△t

D．9+△t

已知函数y=f（x）在（0，1）内的一段图象是如图所示的一段圆弧，若0＜x₁＜x₂＜1，则（ ）

A．＜

B．=

C．＞

D．不能确定

一物体的运动方程为s=t+t²，其中s的单位是米，t的单位是秒，那么物体在3秒末的瞬时速度为（ ）

A．3米/秒

B．5米/秒

C．7米/秒

D．9米/秒

若函数f（x）=2x²﹣1的图象上一点（1，1）及邻近一点（1+△x，1+△y），则等于（ ）

A．4

B．4x

C．4+2△x

D．4+2△x^2

设函数f（x）在点x₀可导，则=（ ）

A．f′（x0）

B．f′（x0）

C．2f′（x0）

D．不存在

在圆x²+y²﹣5y=0内，过点作n条弦（n∈N⁺），它们的长构成等差数列{a_n}，若a₁为过该点最短的弦，a_n为过该点最长的弦，且公差，则n的值为（ ）

A．4

B．5

C．6

D．7

把70个面包分5份给5个人，使每人所得成等差数列，且使较大的三份之和的是较小的两份之和，问最小的1份为．（ ）

A．2

B．8

C．14

D．20

定义：在数列{a_n}中，若满足﹣=d（n∈N⁺，d 为常数），称{a_n}为“等差比数列”．已知在“等差比数列”{a_n}中，a₁=a₂=1，a₃=3，则=（ ）

A．4×2012^2﹣1

B．4×2013^2﹣1

C．4×2014^2﹣1

D．4×2013^2