北师大版必修五 1.4数列在日常经济生活中应用练习卷
《莱因德纸草书》是世界上最古老的数学著作之一.书中有一道这样的题目:把100个面包分给五个人,使每人所得成等差数列,且使较大的三份之和的 是较小的两份之和,问最小1份为( )
是较小的两份之和,问最小1份为( )
A.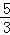 |
B.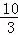 |
C.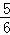 |
D.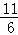 |
设a>1,定义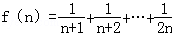 ,如果对任意的n∈N*且n≥2,不等式12f(n)+7logab>7loga+1b+7(a>0且a≠1)恒成立,则实数b的取值范围是( )
,如果对任意的n∈N*且n≥2,不等式12f(n)+7logab>7loga+1b+7(a>0且a≠1)恒成立,则实数b的取值范围是( )
A.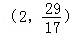 |
B.(0,1) | C.(0,4) | D.(1,+∞) |
已知数列{an}是各项均为正数且公比不等于1的等比数列.对于函数y=f(x),若数列{lnf(an)}为等差数列,则称函数f(x)为“保比差数列函数”.现有定义在(0,+∞)上的如下函数:
① ,
,
②f(x)=x2,
③f(x)=ex,
④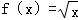 ,
,
则为“保比差数列函数”的所有序号为( )
| A.①② | B.③④ | C.①②④ | D.②③④ |
某辆汽车购买时的费用是15万元,每年使用的保险费、路桥费、汽油费等约为1.5万 元.年维修保养费用第一年3000元,以后逐年递增3000元,则这辆汽车报废的最佳年 限(即使用多少年的年平均费用最少)是( )
| A.8 年 | B.1O 年 | C.12 年 | D.15 年 |
已知数列{an}(n∈N*)是各项均为正数且公比不等于1的等比数列,对于函数y=f(x),若数列{1nf(an)}为等差数列,则称函数f(x)为“保比差数列函数”.现有定义在(0,+∞)上的三个函数:①f(x)= ;②f(x)=ex ③f(x)=
;②f(x)=ex ③f(x)=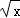 ,则为“保比差数列函数”的是( )
,则为“保比差数列函数”的是( )
| A.①② | B.②③ | C.①③ | D.①②③ |
定义:在数列{an}中,若满足 ﹣
﹣ =d(n∈N+,d 为常数),称{an}为“等差比数列”.已知在“等差比数列”{an}中,a1=a2=1,a3=3,则
=d(n∈N+,d 为常数),称{an}为“等差比数列”.已知在“等差比数列”{an}中,a1=a2=1,a3=3,则 =( )
=( )
| A.4×20122﹣1 | B.4×20132﹣1 | C.4×20142﹣1 | D.4×20132 |
在圆x2+y2﹣5y=0内,过点 作n条弦(n∈N+),它们的长构成等差数列{an},若a1为过该点最短的弦,an为过该点最长的弦,且公差
作n条弦(n∈N+),它们的长构成等差数列{an},若a1为过该点最短的弦,an为过该点最长的弦,且公差 ,则n的值为( )
,则n的值为( )
| A.4 | B.5 | C.6 | D.7 |
以(0,m)间的整数(m>1),m∈N)为分子,以m为分母组成分数集合A1,其所有元素和为a1;以(0,m2)间的整数(m>1),m∈N)为分子,以m2为分母组成不属于集合A1的分数集合A2,其所有元素和为a2;…,依此类推以(0,mn)间的整数(m>1,m∈N)为分子,以mn为分母组成不属于A1,A2,…,An﹣1的分数集合An,其所有元素和为an;则a1+a2+…+an= .
将正整数1,2,3,4,…,n2(n≥2)任意排成n行n列的数表,对于某一个数表,计算各行和各列中的任意两个数a,b(a>b)的比值 ,称这些比值中的最小值为这个数表的“特征值”,记为f(n).若aij表示某个n行n列数表中第i行第j列的数(1≤i≤n,1≤j≤n),且满足aij=
,称这些比值中的最小值为这个数表的“特征值”,记为f(n).若aij表示某个n行n列数表中第i行第j列的数(1≤i≤n,1≤j≤n),且满足aij= ,则:
,则:
(1)f(3)= ;
(2)f(2013)= .
对于实数x,将满足“0≤y<1且x﹣y为整数”的实数y称为实数x的小数部分,用符号<x>表示.对于实数a,无穷数列{an}满足如下条件:
①a1=<a>;
②an+1= .
.
(Ⅰ)若a= 时,数列{an}通项公式为 ;
时,数列{an}通项公式为 ;
(Ⅱ)当a> 时,对任意n∈N*都有an=a,则a的值为 .
时,对任意n∈N*都有an=a,则a的值为 .
定义:对于各项均为整数的数列{an},如果ai+i(i=1,2,3,…)为完全平方数,则称数列{an}具有“P性质”;不论数列{an}是否具有“P性质”,如果存在数列{bn}与{an}不是同一数列,且{bn}满足下面两个条件:
(1)b1,b2,b3,…,bn是a1,a2,a3,…,an的一个排列;
(2)数列{bn}具有“P性质”,则称数列{an}具有“变换P性质”.给出下面三个数列:
①数列{an}的前n项和Sn= (n2﹣1);
(n2﹣1);
②数列{bn}:1,2,3,4,5;
③数列{cn}:1,2,3,4,5,6.
具有“P性质”的为 ;具有“变换P性质”的为 .
对于数列{an},规定{△1an}为数列{an}的一阶差分数列,其中△1an=an+1﹣an(n∈N*).对于正整数k,规定{△kan}为{an}的k阶差分数列,其中△kan=△k﹣1an+1﹣△k﹣1an.若数列{an}有a1=1,a2=2,且满足△2an+△1an﹣2=0(n∈N*),则a14= .
粗细都是1cm一组圆环依次相扣,悬挂在某处,最上面的圆环外直径是20cm,每个圆环的外直径皆比它上面的圆环的外直径少1cm. 那么从上向下数第3个环底部与第1个环顶部距离是 ;记从上向下数第n个环底部与第一个环顶部距离是an,则an= .
已知函数f(x)=x+sinx.项数为19的等差数列{an}满足an∈ ,且公差d≠0.若f(a1)+f(a2)+…+f(a18)+f(a19)=0,则当k= 时,f(ak)=0.
,且公差d≠0.若f(a1)+f(a2)+…+f(a18)+f(a19)=0,则当k= 时,f(ak)=0.
 是较小的两份之和,问最小的1份为.( )
是较小的两份之和,问最小的1份为.( )
 ,其前n项和是Sn,对任意的m,n∈N*且m<n,则Sn﹣Sm的最大值是 .
,其前n项和是Sn,对任意的m,n∈N*且m<n,则Sn﹣Sm的最大值是 . 的最小正整数n是 .
的最小正整数n是 . 对任何等差数列{an}及任何正整数n恒成立,则λ的最大值为 .
对任何等差数列{an}及任何正整数n恒成立,则λ的最大值为 . 粤公网安备 44130202000953号
粤公网安备 44130202000953号