将正整数1，2，3，4，…，n2（n≥2）任意排成n行n列的数表，对于某一个数表，计算各行和各列中的任意两个数a，b（a＞b）的比值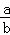
，称这些比值中的最小值为这个数表的“特征值”，记为f（n）．若aij表示某个n行n列数表中第i行第j列的数（1≤i≤n，1≤j≤n），且满足aij=
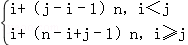，则：
（1）f（3）= ；
（2）f（2013）= ．
相关试题
＝ad－bc，则符合条件
＝2的复数z＝________.
x－1＝10i－ix－2ix2有实数根，则实数a的值为______．
＝________.推荐套卷
将正整数1，2，3，4，…，n2（n≥2）任意排成n行n列的数表，对于某一个数表，计算各行和各列中的任意两个数a，b（a＞b）的比值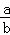，称这些比值中的最小值为这个数表的“特征值”，记为f（n）．若aij表示某个n行n列数表中第i行第j列的数（1≤i≤n，1≤j≤n），且满足aij=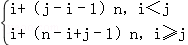，则：
（1）f（3）= ；
（2）f（2013）= ．
粤公网安备 44130202000953号