北师大版选修1-1 3.1变化的快慢与变化率练习卷
路灯距离地面8m,一个身高为1.6m的人以84m/min的速度从路灯在地面上的射影点O沿某直线离开路灯,那么人影长度的变化速率为( )
A. m/s m/s |
B. m/s m/s |
C. m/s m/s |
D. m/s m/s |
有人从“若a<b,则2a< <2b”中找到灵感引入一个新概念,设F(x)=x2,f(x)=2x,于是有f(a)<
<2b”中找到灵感引入一个新概念,设F(x)=x2,f(x)=2x,于是有f(a)< <f(b),此时称F(x)为甲函数,f(x)为乙函数,下面命题正确的是( )
<f(b),此时称F(x)为甲函数,f(x)为乙函数,下面命题正确的是( )
| A.若f(x)=3x2+2x则F(x)=x3+x2+C,C为常数 |
| B.若f(x)=cosx,则F(x)=sinx+C,C为常数 |
| C.若f(x)=x2+1,则F(x)为奇函数 |
| D.若f(x)=ex,则F(2)<F(3)<F(5) |
已知函数f(x),当自变量由x0变化到x1时函数值的增量与相应的自变量的增量比是函数( )
| A.在x0处的变化率 |
| B.在区间[x0,x1]上的平均变化率 |
| C.在x1处的变化率 |
| D.以上结论都不对 |
一直线运动的物体,从时间t到t+△t时,物体的位移为△s,那么 为( )
为( )
| A.从时间t到t+△t时,物体的平均速度 |
| B.时间t时该物体的瞬时速度 |
| C.当时间为△t时该物体的速度 |
| D.从时间t到t+△t时位移的平均变化率 |
f(x)= 的不连续点为( )
的不连续点为( )
| A.x=0 |
B.x= (k=0,±1,±2,…) (k=0,±1,±2,…) |
| C.x=0和x=2kπ(k=0,±1,±2,…) |
D.x=0和x= (k=0,±1,±2,…) (k=0,±1,±2,…) |
设函数y=f(x),当自变量x由x0改变到x0+△x时,函数值的改变量△y等于( )
| A.f(x0+△x) | B.f(x0)+△x |
| C.f(x0)•△x | D.f(x0+△x)﹣f(x0) |
当自变量从x0变到x1时,函数值的增量与相应自变量的增量之比是函数( )
| A.在区间[x0,x1]上的平均变化率 |
| B.在x0处的变化率 |
| C.在x1处的导数 |
| D.在区间[x0,x1]上的导数 |
在高台跳水运动中,已知运动员相对于水面的高度h(单位:m)与起跳后的时间t(单位:s)存在函数关系h(t)=﹣4.9t2+6.5t+10,则运动员在t=1s时的瞬间速度为( )
| A.3.3m/s | B.﹣3.3m/s | C.11.6m/s | D.﹣11.6m/s |
 =( )
=( ) f′(x0)
f′(x0) 等于( )
等于( )
 <
<
 =
=
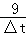

 等于( )
等于( ) f′(x)
f′(x) 两处的瞬时变化率为k1和k2,则k1+k2为( )
两处的瞬时变化率为k1和k2,则k1+k2为( )
 =( )
=( ) 粤公网安备 44130202000953号
粤公网安备 44130202000953号