高中数学组合几何试题

已知f（3）=2，f′（x）=﹣2，则=（ ）

A．﹣4

B．6

C．8

D．不存在

f（x）=的不连续点为（ ）

A．x=0

B．x=（k=0，±1，±2，…）

C．x=0和x=2kπ（k=0，±1，±2，…）

D．x=0和x=（k=0，±1，±2，…）

一直线运动的物体，从时间t到t+△t时，物体的位移为△s，那么为（ ）

A．从时间t到t+△t时，物体的平均速度

B．时间t时该物体的瞬时速度

C．当时间为△t时该物体的速度

D．从时间t到t+△t时位移的平均变化率

设f（x）在x处可导，则等于（ ）

A．2f′（x）

B．f′（x）

C．f′（x）

D．4f′（x）

有人从“若a＜b，则2a＜＜2b”中找到灵感引入一个新概念，设F（x）=x²，f（x）=2x，于是有f（a）＜＜f（b），此时称F（x）为甲函数，f（x）为乙函数，下面命题正确的是（ ）

A．若f（x）=3x^2+2x则F（x）=x^3+x^2+C，C为常数

B．若f（x）=cosx，则F（x）=sinx+C，C为常数

C．若f（x）=x^2+1，则F（x）为奇函数

D．若f（x）=e^x，则F（2）＜F（3）＜F（5）

路灯距离地面8m，一个身高为1.6m的人以84m/min的速度从路灯在地面上的射影点O沿某直线离开路灯，那么人影长度的变化速率为（ ）

A．m/s

B．m/s

C．m/s

D．m/s

某汽车启动阶段的位移函数为s（t）=2t³﹣5t²，则汽车在t=2时的瞬时速度为（ ）

A．10

B．14

C．4

D．6

已知某质点的位移s与移动时间t满足s=t²•e^t﹣2，则质点在t=2的瞬时速度是（ ）

A．4

B．6

C．8

D．16

已知函数（为无理数，）
（1）求函数在点处的切线方程；
（2）设实数，求函数在上的最小值；
（3）若为正整数，且对任意恒成立，求的最大值．

已知．
（1）若，求曲线在点处的切线方程；
（2）若 求函数的单调区间．

设函数f（x）＝－ax，g（x）＝b＋2b－1．
（1）若曲线y＝f（x）与y＝g（x）在它们的交点（1，c）处有相同的切线，求实数a，b的值；
（2）当a＝1，b＝0时，求函数h（x）＝f（x）＋g（x）在区间[t，t＋3]内的最小值．

已知函数的定义域是D，关于函数给出下列命题：
①对于任意，函数是D上的减函数；
②对于任意，函数存在最小值；
③对于任意，使得对于任意的，都有＞0成立；
④对于任意，使得函数有两个零点；
其中正确命题的序号是__________（写出所有正确命题的序号）。

已知函数，曲线上点处的切线方程为.
（1）若在时有极值，求的表达式；
（2）在（1）的条件下求在上的最值及相应的的值.

曲线在横坐标为l的点处的切线为，则点P(3，2)到直线的距离为（  ）

A．

B．

C．

D．

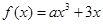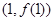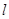设函数，其图象在点处的切线与直线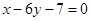垂直，则直线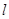与坐标轴围成的三角形的面积为（   ）

A．

B．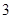

C．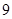

D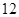．