函数y= -x2+1(0<x<2)的图象上任意点处切线的倾斜角记为α,则α的最小值是( )
-x2+1(0<x<2)的图象上任意点处切线的倾斜角记为α,则α的最小值是( )
A. |
B. |
C. |
D. |
已知函数 在点
在点 处的切线方程为
处的切线方程为 .
.
⑴求函数 的解析式;
的解析式;
⑵若对于区间 上任意两个自变量的值
上任意两个自变量的值 都有
都有 ,求实数
,求实数 的最小值;
的最小值;
⑶若过点 可作曲线
可作曲线 的三条切线,求实数
的三条切线,求实数 的取值范围.
的取值范围.
曲线 轴于点A,△OAB(O是原点)是以A为顶点的等腰三角形,则切线l的倾斜角为 ( )
轴于点A,△OAB(O是原点)是以A为顶点的等腰三角形,则切线l的倾斜角为 ( )
| A.30° | B.45° | C.60° | D.120° |
已知函数 ∈R).
∈R).
(1)若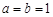 ,求
,求 点(
点(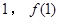 )处的切线方程;
)处的切线方程;
(2)设a≤0,求 的单调区间;
的单调区间;
(3)设a<0,且对任意的 ,
, ≤
≤ ,试比较
,试比较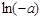 与
与 的大小.
的大小.