设函数
,曲线
在点
处的切线方程为
.
(Ⅰ)求
的解析式:
(Ⅱ)证明:函数
的图像是一个中心对称图形,并求其对称中心;
(Ⅲ)证明:曲线
上任一点的切线与直线
和直线
所围三角形的面积为定值,并求出此定值.
下面关于 的判断:
的判断: 与
与 的图象关于直线
的图象关于直线 对称;
对称;
若 为偶函数,且
为偶函数,且 ,则
,则 的图象关于直线
的图象关于直线 对称;
对称;
设函数 ,且
,且 ,
, ,
, ,若
,若 ,则
,则
函数 ,
, ,
, ,
, ,存在
,存在 ,
, ,使得
,使得 .
.
其中正确的判断是____ _____(把你认为正确的判断都填上)
已知函数 ∈R).
∈R).
(1)若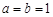 ,求
,求 点(
点(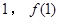 )处的切线方程;
)处的切线方程;
(2)设a≤0,求 的单调区间;
的单调区间;
(3)设a<0,且对任意的 ,
, ≤
≤ ,试比较
,试比较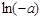 与
与 的大小.
的大小.