高中数学表面展开图填空题

如图，在直四棱柱中，点分别在上，且，，点到的距离之比为3：2，则三棱锥和的体积比=" __" ___.

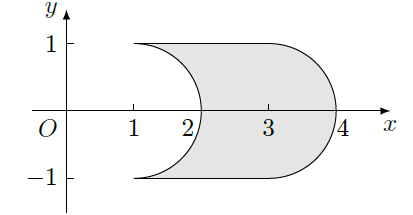
在 $xOy$平面上，将两个半圆弧 $(x-1{)}^2+y^2=1(x\ge 1)$和 $(x-3{)}^2+y^2=1(x\ge 3)$、两条直线 $y=1$和 $y=-1$围成的封闭图形记为 $D$，如图中阴影部分．记 $D$绕 $y$轴旋转一周而成的几何体为Ω，过 $(0,y)(\left|y\right|\le 1)$作Ω的水平截面，所得截面面积为 $4\pi \sqrt{1-y^2}+8\pi$，试利用祖暅原理、一个平放的圆柱和一个长方体，得出Ω的体积值为.

若一个底面边长为 $\frac{\sqrt{3}}{2}$，棱长为 $\sqrt{6}$的正六棱柱的所有顶点都在一个平面上，则此球的体积为．

如图1，在棱长为的正方体中，P、Q是对角
线上的点，若，则三棱锥的体积为 ________

正四棱台的上、下两底面边长分别为3和6，其侧面积等于两底面积之和，则四棱台的高为_____________.

在四面体ABCD中，，则四面体的外接球的体积为   ▲ .

已知一个球的内接正方体的表面积为S，那么这个球的半径为         ．

平面内，两个正三角形的边长比为，则其外接圆的面积比为；类似地，空间中,两个正四面体的棱长比为,则其外接球的体积比为.

设直线与球O有且仅有一公共点P，从直线出发的两个半平面截球O的两个截面圆O₁和圆O₂的半径1和2，若这两个半平面，所成二面角为120⁰，则球O的表面积为    。

一个凸多面体的三视图如图所示，则这个凸多面体的体积是__ __。

某圆锥体的侧面展开图是半圆，当侧面积是时，则该圆锥体的体积是     ．

将函数与y＝3的图象所围成的封闭图形绕x轴旋转一周，则所得旋转体的表
面积为    .

一个几何的三视图如图所示：其中，正视图中△ABC的边长是2的正三角形，俯视图为正六边形，那么该几何体几的体积为                 .

已知为球的半径，过的中点且垂直于的平面截球面得到圆，若圆的面积为，则球的表面积等于。

直三棱柱 $ABC-A_1{B}_1{C}_1$的各顶点都在同一球面上，若 $AB=AC=A{A}_1=2$, $\angle BAC=120°$，则此球的表面积等于.