(本小题满分12分)请你设计一个包装盒,如下 图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A、B、C、D四个点重合于图中的点P,正好形成一个正四棱挪状的包装盒E、F在AB上,是被切去的一等腰直角三角形斜边的两个端点.设AE= FB=x(
图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A、B、C、D四个点重合于图中的点P,正好形成一个正四棱挪状的包装盒E、F在AB上,是被切去的一等腰直角三角形斜边的两个端点.设AE= FB=x( cm).
cm).
(I)某广告商要求包装盒的侧面积S(cm2) 最大,试问x应取何值?
最大,试问x应取何值?
(II)某厂商要求包装盒的容积V(cm3)最大,试问x应取何值?并求出此时包装盒的高与底面边长的比值.[
(本题满分 8 分)如图,正四棱柱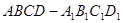 的底面边长
的底面边长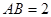 ,若异面直线
,若异面直线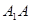 与
与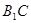 所成角的大小为
所成角的大小为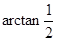 ,求正四棱柱
,求正四棱柱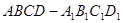 的体积.
的体积.
如右图所示,在正三棱柱ABC—A1B1C1中,AB=3,AA1=4,M为AA1的中点,P是BC上一点,且由P沿棱柱侧面经过棱CC1到M的最短路线长为,设这条最短路线与CC1的交点为N.求:
(1)该三棱柱的侧面展开图的对角线长;
(2)PC和NC的长.
(本小题满分12分)在长方体 中,
中, ,过
,过 ,
, ,
, 三点的平面截去长方体的一个角后,得到如图所示的几何体
三点的平面截去长方体的一个角后,得到如图所示的几何体 ,这个几何体的体积为
,这个几何体的体积为 。
。
(1)求棱 的长;
的长;
(2)求经过 ,
, ,
, ,
, 四点的球的表面积。
四点的球的表面积。
如图是某直三棱柱被削去上底后的直观图与三视图的侧视图、俯视图,在直观图中,M是BD的中点,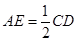 ,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示。
,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示。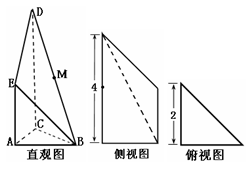
(Ⅰ)求出该几何体的体积;
(Ⅱ)试问在边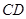 上是否存在点N,使
上是否存在点N,使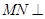 平面
平面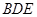 ? 若存在,确定点N的位置(不需证明);若不存在,请说明理由。
? 若存在,确定点N的位置(不需证明);若不存在,请说明理由。
已知某几何体的俯视图是如图1所示的矩形,正视图(或称主视图)是一个底边长为8,高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6,高为4的等腰三角形.
(Ⅰ)求该几何体的体积 ;
;
(Ⅱ)求该几何体的侧面积 .
.
用长为18m的钢条围成一个长方体形状的框架,要求长方体的长与宽之比为2:1,问该长方体的长、宽、高各为多少时,其体积最大?最大体积是多少?
如图,在直角梯形 中,
中, ,
, ,且
,且 .现以
.现以 为一边向梯形外作矩形
为一边向梯形外作矩形 ,然后沿边
,然后沿边 将矩形
将矩形 翻折,使平面
翻折,使平面 与平面
与平面 垂直.
垂直.
(1)求证: 平面
平面 ;
;
(2)若点 到平面
到平面 的距离为
的距离为 ,求三棱锥
,求三棱锥 的体积.
的体积.
(本小题满分12分)如图,多面体ABCDEF中,底面ABCD是菱形, ,四边形BDEF是正方形,且
,四边形BDEF是正方形,且 平面ABCD.
平面ABCD.
(Ⅰ)求证: 平面AED;
平面AED;
(Ⅱ)若 ,求多面体ABCDEF的体积V.
,求多面体ABCDEF的体积V.
(本小题满分12分)如图,在斜三棱柱 中,侧面
中,侧面 与侧面
与侧面 都是菱形,
都是菱形, ,
, .
.
(Ⅰ)求证: ;
;
(Ⅱ)若 ,求四棱锥
,求四棱锥 的体积.
的体积.
(本小题满分14分))如图,在三棱柱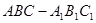 中,
中, ⊥底面
⊥底面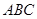 ,且△
,且△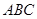 为正三角形,
为正三角形,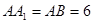 ,
,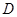 为
为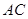 的中点.
的中点.
(1)求证:直线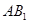 ∥平面
∥平面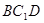 ;
;
(2)求证:平面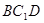 ⊥平面
⊥平面 ;
;
(3)求三棱锥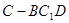 的体积.
的体积.