已知正三角形 三个顶点都在半径为
三个顶点都在半径为 的球面上,球心
的球面上,球心 到平面
到平面 的距离为
的距离为 ,点
,点 是线段
是线段 的中点,过点
的中点,过点 作球
作球 的截面,则截面面积的最小值是()
的截面,则截面面积的最小值是()
A. |
B. |
C. |
D. |
将一张边长为6 cm的纸片按如图l所示阴影部分裁去四个全等的等腰三角形,将余下部分沿虚线折叠并拼成一个有底的正四棱锥(底面是正方形,顶点在底面的射影为正方形的中心)模型,如图2放置.若正四棱锥的正视图是正三角形(如图3),则正四棱锥的体积是()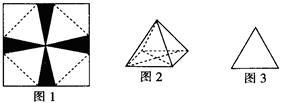
A. |
B.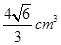 |
C. |
D. |
(本小题满分12分)如图四边形ABCD为菱形,G为AC与BD交点, ,
,
(1)证明:平面 平面
平面 ;
;
(2)若 ,
,
 ,令AE与平面ABCD所成角为
,令AE与平面ABCD所成角为 ,且
,且 ,求该四棱锥
,求该四棱锥 的体积.
的体积.
已知直三棱柱 中,
中, ,侧面
,侧面 的面积为
的面积为 ,则直三棱柱
,则直三棱柱 外接球表面积的最小值为 .
外接球表面积的最小值为 .
已知直三棱柱 中,
中, ,侧面
,侧面 的面积为
的面积为 ,则直三棱柱
,则直三棱柱 外接球表面积的最小值为 .
外接球表面积的最小值为 .
(本小题满分12分)如图,矩形 中,对角线
中,对角线 的交点为
的交点为 ⊥平面
⊥平面
 为
为 上的点,且
上的点,且 .
.
(I)求证: ⊥平面
⊥平面 ;
;
(II)求三棱锥 的体积.
的体积.
已知三棱锥 ,
, 两两垂直且长度均为6,长为2的线段
两两垂直且长度均为6,长为2的线段 的一个端点
的一个端点 在棱
在棱 上运动,另一个端点
上运动,另一个端点 在
在 内运动(含边界),则
内运动(含边界),则 的中点
的中点 的轨迹与三棱锥的面所围成的几何体的体积为
的轨迹与三棱锥的面所围成的几何体的体积为
A. |
B. 或 或 |
C. |
D. 或 或 |
(本小题满分12分)如图,在三棱锥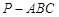 中,
中, 丄平面
丄平面 ,
,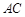 丄
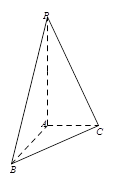
丄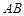 ,
, ,
, .
.
(Ⅰ)证明: 丄
丄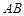 ;
;
(Ⅱ)求二面角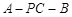 的正弦值;
的正弦值;
(Ⅲ)求三棱锥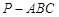 外接球的体积.
外接球的体积.
(本题14分)一个圆锥的底面半径为 ,高为
,高为 ,其中有一个高为
,其中有一个高为 的内接圆柱:
的内接圆柱:
(1)求圆锥的侧面积;
(2)当 为何值时,圆柱侧面积最大?并求出最大值.
为何值时,圆柱侧面积最大?并求出最大值.