若命题: ∈R,
∈R, -2ax+a≤0”为假命题,则
-2ax+a≤0”为假命题,则 的最小值是__________.
的最小值是__________.
若对任意x∈R,y∈R有唯一确定的f (x,y)与之对应,则称f (x,y)为关于x,y的二元函数.定义:同时满足下列性质的二元函数f (x,y)为关于实数x,y的广义“距离”:
(Ⅰ)非负性:f (x,y)≥0;
(Ⅱ)对称性:f (x,y)= f (y,x);
(Ⅲ)三角形不等式:f (x,y)≤f (x,z)+ f (z,y)对任意的实数z均成立.
给出下列二元函数:
①f (x,y)=(x-y)2;②f (x,y)=|x-y|;③f (x,y)= ;④f (x,y)=|sin(x-y)|.
;④f (x,y)=|sin(x-y)|.
则其中能够成为关于x,y的广义“距离”的函数编号是______.(写出所有真 命题的序号)
命题的序号)
定义: 表示
表示 两个数中的最大值,
两个数中的最大值, 表示
表示 两个数中的最小值。给出下列4个命题:
两个数中的最小值。给出下列4个命题:
①
 且
且 ;
;
②
 且
且 ;
;
③设函数 和
和 的公共定义域为
的公共定义域为 ,若
,若 ,
, 恒成立,则
恒成立,则 ;
;
④若函数 的图像关于直线
的图像关于直线 对称,则
对称,则 的值为
的值为 。
。
其中真命题是 。(写出所有真命题的序号)
关与直线m,n与平面M,N,有以下四个命题:
(1)若m//M,n//N且M⊥N,则m//n;
(2)若m⊥M,n⊥N,且M⊥N,则m⊥n;
(3)若m⊥M,n//N且M//N,则m⊥n;
(4)若M//N且m与平面M所成的角等于n与平面N所成的角,则m//n.
其中真命题的序号是_____________________。
以下四个命题中:
①从匀速传递的产品生产流水线上,质检员每10分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样;
②两个随机变量的线性相关性越强,相关系数的绝对值越接近于1;
③某项测量结果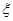 服从正太态布
服从正太态布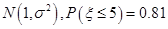 ,则
,则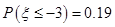 ;
;
④对于两个分类变量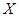 和
和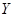 的随机变量
的随机变量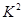 的观测值
的观测值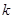 来说,
来说,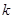 越小,判断“
越小,判断“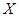 与
与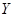 有关系”的把握程度越大.
有关系”的把握程度越大.
以上命题中其中真命题的个数为 .
下列4个命题:
①“如果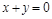 ,则
,则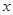 、
、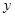 互为相反数”的逆命题
互为相反数”的逆命题
②“如果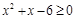 ,则
,则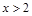 ”的否命题
”的否命题
③在△ABC中,“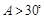 ”是“
”是“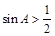 ”的充分不必要条件
”的充分不必要条件
④“函数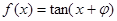 为奇函数”的充要条件是“
为奇函数”的充要条件是“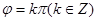 ”
”
其中真命题的序号是 .
设非空集合 ,若对
,若对 中任意两个元素
中任意两个元素 ,
,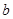 ,通过某个法则“
,通过某个法则“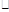 ”,使
”,使 中有唯一确定的元素
中有唯一确定的元素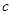 与之对应,则称法则“
与之对应,则称法则“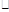 ”为集合
”为集合 上的一个代数运算。若
上的一个代数运算。若 上的代数运算“
上的代数运算“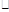 ”还满足:(1)对
”还满足:(1)对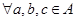 ,都有
,都有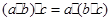 ;(2)对
;(2)对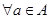 ,
,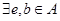 ,使得
,使得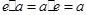 ,
,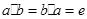 。称
。称 关于法则“
关于法则“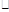 ”构成一个群。给出下列命题:
”构成一个群。给出下列命题:
①实数的除法是实数集上的一个代数运算;
②自然数集关于自然数的加法不能构成一个群;
③非零有理数集关于有理数的乘法构成一个群;
④正整数集关于法则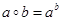 构成一个群。
构成一个群。
其中正确命题的序号是____________。(填上所有正确命题的序号)。