高中数学截面及其作法解答题

已知 且；
集合，且.
若∨为真命题，∧为假命题，求实数的取值范围.

（本小题满分12分）已知命题:在上定义运算：不等式对任意实数恒成立；命题：若不等式对任意的恒成立．若为假命题，为真命题，求实数的取值范围.

已知命题：方程表示的曲线为椭圆；命题：方程表示的曲线为双曲线；若或为真，且为假，求实数的取值范围．

分别写出下列命题的逆命题、逆否命题，并判断它们的真假：
（1）若q＜1，则方程x²+2x+q=0有实根；
（2）若x²+y²=0，则x，y全为零．

设命题；命题：不等式对任意恒成立．若为真，且或为真，求的取值范围．

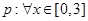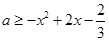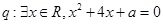已知命题，，命题，若命题“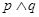”是真命题，求实数a的取值范围．

己知命题：方程表示焦点在轴的椭圆；命题：关于的不等式的解集是R；若“” 是假命题，“”是真命题，求实数的取值范围。

已知命题p：“任意的x∈[1,2]，x²－a≥0”；
命题q：“存在x₀∈R，x₀²＋2ax₀＋2－a＝0”，若命题“p且q”是真命题．
求实数a的取值范围．

命题： ；命题：。
若为假命题，为假命题，则求的取值范围。

已知命题p：若，则x=2且y=﹣1．
（1）写出p的否命题q，并判断q的真假（不必写出判断过程）；
（2）写出p的逆否命题r，并判断r的真假（不必写出判断过程）．

设命题p：;命题q: ，若是的必要不充分条件，
（1）p是q的什么条件？      
（2）求实数a的取值范围．

设命题p:|2^x-3|＜1;命题q：lg²x - （2t+l）lgx+t（t+l）≤0，
（1）若命题q所表示不等式的解集为A={x|l0≤x≤100}，求实数t的值；
（2）若p是q的必要不充分条件，求实数t的取值范围．

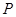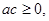已知命题：“若则二次方程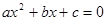没有实根”.
（1）写出命题的否命题；
（2）判断命题的否命题的真假， 并证明你的结论．

（本小题满分15分）知命题，命题，使.若命题“p且q”为真命题，求实数a的取值范围.

设p：，q：关于x的不等式x²－4x＋m²≤0的解集是空集，试确定实数m的取值范围，使得p或q为真命题，p且q为假命题