如图所示:矩形 的一边
的一边 在
在 轴上,另两个顶点
轴上,另两个顶点 在函数
在函数 的图像上(其中点
的图像上(其中点 的坐标为
的坐标为 ),矩形
),矩形 的面积记为
的面积记为 ,则
,则 =" "
=" " 
已知两个正数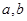 ,可按规则
,可按规则 扩充为一个新数
扩充为一个新数 ,在
,在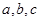 三个数中取两个较大的数,按上述规则扩充得到一个新数,依次下去,将每扩充一次得到一个新数称为一次操作.
三个数中取两个较大的数,按上述规则扩充得到一个新数,依次下去,将每扩充一次得到一个新数称为一次操作.
(1)若 ,按上述规则操作三次,扩充所得的数是__________;
,按上述规则操作三次,扩充所得的数是__________;
(2)若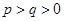 ,经过6次操作后扩充所得的数为
,经过6次操作后扩充所得的数为 (
( 为正整数),则
为正整数),则 的值分别为____________
的值分别为____________
某公司购买一批机器投入生产,据市场分析每台机器生产的产品可获得的总利润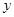 (万元)与机器运转时间
(万元)与机器运转时间 (年数,
(年数,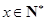 )的关系为
)的关系为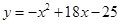 .则当每台机器运转 年时,年平均利润最大,最大值是 万元.
.则当每台机器运转 年时,年平均利润最大,最大值是 万元.
若函数 ,
, 同时满足下列条件,
同时满足下列条件,
(1) 在D内为单调函数;(2)存在实数m,n.当 时,
时, ,则称此函数为D内等射函数,设
,则称此函数为D内等射函数,设
 则:①
则:① 在
在 的单调性为 ;②当
的单调性为 ;②当 为R内的等射函数时,
为R内的等射函数时, 的取值范围是 .
的取值范围是 .
有10台型号相同的联合收割机,收割一片土地上的庄稼.现有两种工作方案:第一种方案,同时投入并连续工作至收割完毕;第二种方案,每隔相同时间先后投入,每一台投入后都连续工作至收割完毕.若采用第一种方案需要24小时,而采用第二种方案时,第一台投入工作的时间恰好为最后一台投入工作时间的5倍,则采用第二种方案时第一台收割机投入工作的时间为 小时.