[北京]2012届北京市朝阳区高三上学期期末考试理科数学
已知正方形 的边长为
的边长为 ,将
,将 沿对角线
沿对角线 折起,使平面
折起,使平面 平面
平面 ,得到如图所示的三棱锥
,得到如图所示的三棱锥 .若
.若 为
为 边的中点,
边的中点, ,
, 分别为线段
分别为线段 ,
, 上的动点(不包括端点),且
上的动点(不包括端点),且 .设
.设 ,则三棱锥
,则三棱锥 的体积
的体积 的函数图象大致是( )
的函数图象大致是( )
A. |
B. |
C. |
D. |
已知集合 ,
,


 .若存在实数
.若存在实数 使得
使得 成立,称点
成立,称点 为“£”点,则“£”点在平面区域
为“£”点,则“£”点在平面区域 内的个数是 ( )
内的个数是 ( )
| A. 0 | B.1 | C.2 | D.无数个 |
已知有若干辆汽车通过某一段公路,从中抽取 辆汽车进行测速分析,其时速的频率分布直方图如图所示,则时速在区间
辆汽车进行测速分析,其时速的频率分布直方图如图所示,则时速在区间 上的汽车大约有 辆.
上的汽车大约有 辆.
某公司购买一批机器投入生产,据市场分析每台机器生产的产品可获得的总利润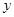 (万元)与机器运转时间
(万元)与机器运转时间 (年数,
(年数,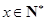 )的关系为
)的关系为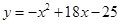 .则当每台机器运转 年时,年平均利润最大,最大值是 万元.
.则当每台机器运转 年时,年平均利润最大,最大值是 万元.
已知两个正数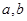 ,可按规则
,可按规则 扩充为一个新数
扩充为一个新数 ,在
,在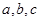 三个数中取两个较大的数,按上述规则扩充得到一个新数,依次下去,将每扩充一次得到一个新数称为一次操作.
三个数中取两个较大的数,按上述规则扩充得到一个新数,依次下去,将每扩充一次得到一个新数称为一次操作.
(1)若 ,按上述规则操作三次,扩充所得的数是__________;
,按上述规则操作三次,扩充所得的数是__________;
(2)若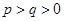 ,经过6次操作后扩充所得的数为
,经过6次操作后扩充所得的数为 (
( 为正整数),则
为正整数),则 的值分别为____________
的值分别为____________
如图,一个圆形游戏转盘被分成6个均匀的扇形区域.用力旋转转盘,转盘停止转动时,箭头A所指区域的数字就是每次游戏所得的分数(箭头指向两个区域的边界时重新转动),且箭头A指向每个区域的可能性都是相等的.在一次家庭抽奖的活动中,要求每个家庭派一位儿童和一位成人先后分别转动一次游戏转盘,得分情况记为 (假设儿童和成人的得分互不影响,且每个家庭只能参加一次活动).
(假设儿童和成人的得分互不影响,且每个家庭只能参加一次活动).
(Ⅰ)求某个家庭得分为 的概率?
的概率?
(Ⅱ)若游戏规定:一个家庭的得分为参与游戏的两人得分之和,且得分大于等于8的家庭可以获得一份奖品.请问某个家庭获奖的概率为多少?
(Ⅲ)若共有5个家庭参加家庭抽奖活动.在(Ⅱ)的条件下,记获奖的家庭数为 ,求
,求 的分布列及数学期望.
的分布列及数学期望.
已知函数 (
( ,
, 为正实数).
为正实数).
(Ⅰ)若 ,求曲线
,求曲线 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)求函数 的单调区间;
的单调区间;
(Ⅲ)若函数 的最小值为
的最小值为 ,求
,求 的取值范围.
的取值范围.
已知椭圆 的离心率为
的离心率为 ,直线
,直线 过点
过点 ,
, ,且与椭圆
,且与椭圆 相切于点
相切于点 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)是否存在过点 的直线
的直线 与椭圆
与椭圆 相交于不同的两点
相交于不同的两点 、
、 ,使得
,使得 ?若存在,试求出直线
?若存在,试求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
 ,
, ,且
,且 ⊥
⊥ ,则实数
,则实数 的值为( )
的值为( )



 ,
, ,若
,若 ,则实数
,则实数




 是公差不为0的等差数列,
是公差不为0的等差数列, 且
且 成等比数列,则
成等比数列,则 项和
项和 等于( )
等于( )



 值为( )
值为( )




 ,设
,设 ,
, ,
, ,则
,则 的大小关系是( )
的大小关系是( )



 的一个零点在区间
的一个零点在区间 内,则实数
内,则实数 的取值范围是( )
的取值范围是( )




 所表示的平面区域的面积是9,则实数
所表示的平面区域的面积是9,则实数 的值为 .
的值为 .  与圆
与圆 相交于
相交于 ,
, 两点,且弦
两点,且弦 的长为
的长为 ,则实数
,则实数 的值是 .
的值是 . 中,
中, ,
, ,
, 分别为内角
分别为内角 ,
, ,
, 所对的边,且满足
所对的边,且满足 .
. ,且
,且 ,
, ,求
,求 的值.
的值. 中,平面
中,平面 平面
平面 .底面
.底面 ,
, .
. ;
; 的大小.
的大小.
 ,
, (
( )由下列条件确定:①
)由下列条件确定:① ;②当
;②当 时,
时, 与
与 满足:当
满足:当 时,
时, ,
, ;当
;当 时,
时, ,
, .
. ,
, ,写出
,写出 ,并求数列
,并求数列 的通项公式;
的通项公式;  (
( ,且
,且 ),试用
),试用 表示
表示
 ;
;
 满足
满足 ,
, ,
, (其中
(其中 为给定的不小于2的整数),求证:当
为给定的不小于2的整数),求证:当 时,恒有
时,恒有 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号