高中数学三面角、直三面角的基本性质试题

某种动物繁殖量（只）与时间（年）的关系为,设这种动物第2年有100只,到第8年它们发展到（   ）

A．200只

B．300只

C．400只

D．500只

已知函数，设。
（Ⅰ）求F（x）的单调区间；
（Ⅱ）若以）图象上任意一点为切点的切线的斜率 恒
成立，求实数的最小值。
（Ⅲ）是否存在实数，使得函数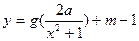的图象与的图象恰
好有四个不同的交点？若存在，求出的取值范围，若不存在，说明理由。来

已知且，则使方程有解时  
的的取值范围为____________

设a、b是不共线的的两向量，其夹角是θ，若函数f（x）=（xa+b）·（a-xb）(xR)在(0, +)上有最大值，则

A．∣a∣＜∣b∣，且θ是钝角	B．∣a∣＜∣b∣，且θ是锐角
C．∣a∣＞∣b∣，且θ是钝角	D．∣a∣＞∣b∣，且θ是锐角

设函数，则=                  。

某公司在甲、乙两地销售一种品牌车，利润（单位：万元）分别为L₁=5．06x-0．15x²
和L₂=2x,其中x为销售量（单位：辆），若该公司在这两地共销售15辆车，则能获得的最大
利润为（   ）

A．45．606

B．45．6

C．45．56

D．45．51

(本小题满分13分)
已知二次函数，且．
（1）若函数与x轴的两个交点之间的距离为2，求b的值；
（2）若关于x的方程的两个实数根分别在区间内，求b的取值范围．

函数，对任意，总有，则（ ）

A．0

B．2

C．

D．28

已知函数，若，则（   ）

A．0

B．1

C．-1

D．

要得到函数的图象，只需要把函数的图象（  ）

A．向左平移2个单位	B．向右平移2个单位
C．向左平移6个单位	D．向右平移6个单位

已知指数函数满足：，定义域为的函数
是奇函数。（1）求的解析式；
（2）求m，n的值；
（3）若对任意的，不等式恒成立，求实数的取值范围。

已知函数, 数列满足，且
数列是单调递增数列，则实数的取值范围是            ．

已知，若，则的取值范围是       ．

在平面直角坐标系中，设二次函数（）的图象与两个坐标轴有三个交点．经过三个交点的圆记为．
（1）求实数b的取值范围；
（2）求圆的方程；

我们把形如的函数因其图像类似于汉字“囧”字，故生动地称为
“囧函数”，并把其与轴的交点关于原点的对称点称为“囧点”，以“囧点”为圆心凡是与“囧函数”有公共点的圆，皆称之为“囧圆”，则当，时，所有的“囧圆”中，面积的最小值为