设函数f(x)的定义域为D,若存在非零实数l使得对于任意x∈M(M⊆D),有x+l∈D,且f(x+l)≥f(x),则称函数f(x)为M上的l高调函数.现给出下列命题:
①函数f(x)=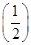 x是R上的1高调函数;
x是R上的1高调函数;
②函数f(x)=sin 2x为R上的π高调函数;
③如果定义域为[-1,+∞)的函数f(x)=x2为[-1,+∞)上的m高调函数,那么实数m的取值范围是[2,+∞).
其中正确的命题是________.(写出所有正确命题的序号)
定义在 上的偶函数,
上的偶函数,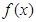 满足
满足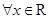 ,都有
,都有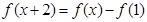 ,且当
,且当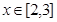 时,
时,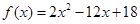 .若函数
.若函数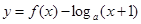 在
在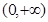 上有三个零点,则
上有三个零点,则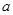 的取值范围是 .
的取值范围是 .
如图放置的边长为1的正方形PABC沿x轴滚动。设顶点P(x,y)的轨迹方程是 ,则
,则 的最小正周期为 ;
的最小正周期为 ; 在其两个相邻零点间的图像与x轴所围区域的面积为 。
在其两个相邻零点间的图像与x轴所围区域的面积为 。

定义在 上的偶函数
上的偶函数 满足
满足 ,且在
,且在 上是增函数,下面是关于f(x)的判断
上是增函数,下面是关于f(x)的判断 :
:
① 关于点P(
关于点P( )对称 ②
)对称 ② 的图像关于直线
的图像关于直线 对称;
对称;
③ 在[0,1]上是增函数; ④
在[0,1]上是增函数; ④ .
.
其中正确的判断是_____________________(把你认为正确的判断都填上)