高中数学三面角、直三面角的基本性质试题

设函数，其中，
（1）证明：是上的减函数；
（2）解不等式

已知两个正数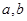,可按规则扩充为一个新数,在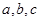三个数中取两个较大的数,按上述规则扩充得到一个新数，依次下去，将每扩充一次得到一个新数称为一次操作.
（1）若,按上述规则操作三次,扩充所得的数是__________；
（2）若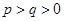，经过6次操作后扩充所得的数为（为正整数），则的值分别为____________

已知函数.
（Ⅰ）讨论函数的单调性；
（Ⅱ）若对任意及时，恒有成立，求实数的取值范围.

方程3x²－e^x=0的实根    (     )

A．不存在

B．有一个

C．有二个

D．有三个

已知函数满足。则=            

方程X－1＝lgX必有一个根的区间是(     )

A．(0. 1, 0. 2)

B．(0. 2, 0. 3)

C．(0. 3, 0. 4)

D．(0. 4, 0. 5)

设函数，若关于的方程在上恰好有两个相异实根，则实数的取值范围为______________．

已知函数
（1）解不等式
（2）若.求证：.

已知函数
（1）解不等式；
（2）对于任意的，不等式恒成立，求的取值范围.

已知，其中、为常数，且，若为常数，则的值为     .

函数对于总有≥0 成立，则的取值集合为   　 ．

已知函数
（1）判断函数在上的单调；
（2）若在上的值域是，求的值.

（1）已知，求函数的最大值和最小值；
（2）要使函数在上f (x)恒成立，求a的取值范围.

设f (x)是奇函数，且在（0，＋∞）上是增函数，又f (－3)＝0，则x·f (x)＜0的解集为

A．{x∣－3＜x＜0或x＞3}

B．{x∣x＜－3或0＜x＜3}

C．{x∣x＜－3或x＞3}

D．{x∣－3＜x＜0或0＜x＜3}

若函数f (x)＝ 则不等式f (x)＜4的解集是       ．