高中数学三面角、直三面角的基本性质试题

设函数.
(1) 试问函数f(x)能否在x= 时取得极值？说明理由；
(2) 若a= ，当x∈［,4］时，函数f(x)与g(x)的图像有两个公共点，求c的取值范围.

本小题满分12分）设函数，当点是函数图象上的点时，点是函数图象上的点．
（1）写出函数的解析式；
（2）若当时，恒有，试确定的取值范围；
（3）把的图象向左平移个单位得到的图象，函数，（）在的最大值为，求的值

已知是定义在上的奇函数，且当时不等式成立，若， ，则大小关系是（   ）

A．

B．

C．

D．

、(本小题满分12分)已知函数
（1）若，求的零点；
（2）若函数在区间上有两个不同的零点，求的取值范围。

在平面直角坐标系中,横坐标、纵坐标均为整数的点称为整点，如果函数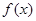的图象恰好通过个整点，则称函数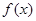为阶整点函数。有下列函数：
；  ②   ③     ④，
其中是一阶整点函数的是(       )

A．①②③④

B．①③④

C．①④

D．④

设Q为有理数集，函数f (x) = g(x)=，则函数h(x)= f (x)·g(x)

A．是奇函数但不是偶函数	B．是偶函数但不是奇函数
C．既是奇函数也是偶函数	D．既不是偶函数也不是奇函数

设函数，判断在上的单调性，并证明.

已知函数
（1）解不等式
（2）若.求证：.

已知函数
（1）解不等式；
（2）对于任意的，不等式恒成立，求的取值范围.

已知，其中、为常数，且，若为常数，则的值为     .

函数对于总有≥0 成立，则的取值集合为   　 ．

已知函数
（1）判断函数在上的单调；
（2）若在上的值域是，求的值.

（1）已知，求函数的最大值和最小值；
（2）要使函数在上f (x)恒成立，求a的取值范围.

设f (x)是奇函数，且在（0，＋∞）上是增函数，又f (－3)＝0，则x·f (x)＜0的解集为

A．{x∣－3＜x＜0或x＞3}

B．{x∣x＜－3或0＜x＜3}

C．{x∣x＜－3或x＞3}

D．{x∣－3＜x＜0或0＜x＜3}

若函数f (x)＝ 则不等式f (x)＜4的解集是       ．