已知函数 ,则下列命题正确的是 .(填上你认为正确的所有命题的序号)
,则下列命题正确的是 .(填上你认为正确的所有命题的序号)
①函数 的最大值为2;
的最大值为2;
②函数 的图象关于点
的图象关于点 对称;
对称;
③函数 的图象与函数
的图象与函数 的图象关于
的图象关于 轴对称;
轴对称;
④若实数 使得方程
使得方程 在
在 上恰好有三个实数解
上恰好有三个实数解 ,则
,则 ;
;
⑤设函数 ,若
,若 ,则
,则 .
.
给出如下五个结论:
①存在α∈(0, ),使sinα+cosα=
),使sinα+cosα= ;
;
②存在区间(a,b),使y=cosx为减函数而sinx<0;
③y=tanx在其定义域内为增函数;
④y=cos2x+sin( -x)既有最大值和最小值,又是偶函数;
-x)既有最大值和最小值,又是偶函数;
⑤y=sin|2x+ |的最小正周期为π.
|的最小正周期为π.
其中正确结论的序号是 .
下列说法中,所有正确说法的序号是 .
①终边在 轴上的角的集合是
轴上的角的集合是 ;
;
②函数 在第一象限是增函数;
在第一象限是增函数;
③函数 的最小正周期是
的最小正周期是 ;
;
④把函数 的图象向右平移
的图象向右平移 个单位长度得到函数
个单位长度得到函数 的图象.
的图象.
给出如下五个结论:
①存在 使
使
②存在区间( )使
)使 为减函数而
为减函数而 <0
<0
③ 在其定义域内为增函数
在其定义域内为增函数
④ 既有最大、最小值,又是偶函数
既有最大、最小值,又是偶函数
⑤ 最小正周期为π
最小正周期为π
其中正确结论的序号是
设 ,其中
,其中 . 若
. 若 对一切
对一切 恒成立,则 ①
恒成立,则 ① ; ②
; ② ;
;
③ 既不是奇函数也不是偶函数;
既不是奇函数也不是偶函数;
④ 的单调递增区间是
的单调递增区间是 ;
;
⑤ 存在经过点 的直线与函数
的直线与函数 的图象不相交.
的图象不相交.
以上结论正确的是__________________(写出所有正确结论的编号).
已知函数 ,给出下列四个说法:
,给出下列四个说法:
① 为奇函数;
为奇函数;
② 的一条对称轴为
的一条对称轴为 ;
;
③ 的最小正周期为
的最小正周期为 ;
;
④ 在区间
在区间 上单调递增;
上单调递增;
⑤ 的图象关于点
的图象关于点 成中心对称.
成中心对称.
其中正确说法的序号是 .
关于函数f(x)=4sin(2x+ ),(x∈R)有下列命题:
),(x∈R)有下列命题:
①y=f(x)是以2π为最小正周期的周期函数;
②y=f(x)可改写为y=4cos(2x﹣ );
);
③y=f(x)的图象关于点(﹣ ,0)对称;
,0)对称;
④y=f(x)的图象关于直线x= 对称;
对称;
其中正确的序号为 .
有下列命题:
①在函数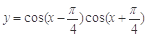 的图象中,相邻两个对称中心的距离为
的图象中,相邻两个对称中心的距离为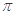 ;
;
②命题:“若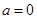 ,则
,则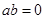 ”的否命题是“若
”的否命题是“若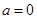 ,则
,则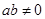 ”;
”;
③“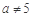 且
且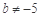 ”是“
”是“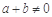 ”的必要不充分条件;
”的必要不充分条件;
④已知命题p:对任意的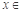 R,都有
R,都有 ,则
,则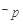 是:存在
是:存在 ,使得
,使得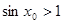 ;
;
⑤命题“若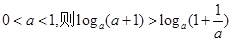 ”是真命题;
”是真命题;
⑥在△ABC中,若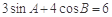 ,
,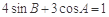 ,则角C等于
,则角C等于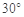 或
或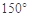 .
.
其中所有真命题的序号是 .
给出下列四个结论:
①存在实数 ,使
,使
②函数 是偶函数
是偶函数
③直线  是函数
是函数 的一条对称轴方程
的一条对称轴方程
④若 都是第一象限的角,且
都是第一象限的角,且 ,则
,则
其中正确结论的序号是____________________.(写出所有正确结论的序号)
有下列命题:①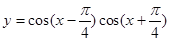 的图象中相邻两个对称中心的距离为
的图象中相邻两个对称中心的距离为 ,②
,② 的图象关于点
的图象关于点 对称,③关于
对称,③关于 的方程
的方程 有且仅有一个实根,则
有且仅有一个实根,则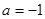 ,④命题
,④命题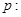 对任意
对任意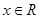 ,都有
,都有 ;则
;则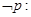 存在
存在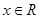 ,使得
,使得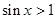 .其中真命题的序号是_________________________ .
.其中真命题的序号是_________________________ .