高中数学几何不等式解答题

仔细阅读下面问题的解法：
设A＝[0，1]，若不等式2^1－x+a>0在A上有解，求实数a的取值范围.
解：令f(x)＝2^1－x+a，因为f(x)>0在A上有解。

＝2+a>0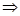a>-2
学习以上问题的解法，解决下面的问题，已知：函数f(x)=x²+2x+3(-2≤x≤-1).
①求f(x)的反函数f^-1(x)及反函数的定义域A；
②设B＝，若A∩B≠,求实数a的取值范围.

（本小题为选做题，满分10分）
设为正数，证明：≥.

某医院用甲、乙两种药片为手术病人配营养餐，已知甲种药片每片含5单位的蛋白质和10单位的铁质，每片售价为3元；乙种药片每片含7单位的蛋白质和4单位的铁质，每片售价2元。若病人每餐至少需要36单位的蛋白质和42单位的铁质，应使用甲、乙两种药片各几片才能既满足营养要求又使费用最省？

已知|a|＜1,|b|＜1,|c|＜1,求证: abc+2＞a+b+c.

已知实数满足，且有
求证：

证明：