设函数 的定义域为
的定义域为 ,若函数
,若函数 满足条件:存在
满足条件:存在
 ,使得
,使得 在区间
在区间 上的值域为
上的值域为
 ,则称
,则称 为“
为“ 倍缩函数”,若函数
倍缩函数”,若函数 为“
为“ 倍缩函数”,则
倍缩函数”,则 的取值范围为( )
的取值范围为( )
A. |
B. |
C. |
D. |
【原创】已知点 ,点
,点 在曲线
在曲线 上,若线段
上,若线段 与曲线
与曲线 相交且交点恰为线段
相交且交点恰为线段 的中点,则称点
的中点,则称点 为曲线
为曲线 与曲线
与曲线 的一个“相关点”,记曲线
的一个“相关点”,记曲线 与曲线
与曲线 的“相关点”的个数为
的“相关点”的个数为 ,则 ( )
,则 ( )
A. |
B. |
C. |
D. |
对于任意x,[x]表示不超过x的最大整数,如[1.1]=1,[﹣2.1]=﹣3,定义R上的函数f(x)=[2x]+[4x]+[8x],若A={y|y=f(x),0≤x≤1},则A中所有元素的和为( )
| A.55 | B.58 | C.63 | D.65 |
设函数 在R上有定义,对于任一给定的正数
在R上有定义,对于任一给定的正数 ,定义函数
,定义函数 ,则称函数
,则称函数 为
为 的“
的“ 界函数”若给定函数
界函数”若给定函数 ,则下列结论不成立的是( )
,则下列结论不成立的是( )
A. |
B. |
C. |
D. |
对于函数 ,若在其定义域内存在两个实数
,若在其定义域内存在两个实数 ,当
,当 时,
时, 的值域也是
的值域也是 ,则称函数
,则称函数 为“科比函数”.若函数
为“科比函数”.若函数 是“科比函数”,则实数
是“科比函数”,则实数 的取值范围
的取值范围
A. |
B. |
C. |
D. |
【原创】设函数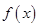 的定义域为
的定义域为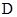 ,如果
,如果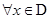 ,
,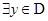 ,使得
,使得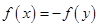 成立,那
成立,那
么称函数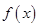 为“
为“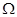 函数”.则下列四个函数中,不属于“
函数”.则下列四个函数中,不属于“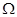 函数”的是( )
函数”的是( )
A.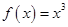 |
B.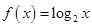 |
C. |
D. |
设函数 在
在 上的最小值为
上的最小值为 ,最大值为
,最大值为 若存在最小正整数
若存在最小正整数 使得
使得
 对任意
对任意 成立,则称函数
成立,则称函数 为区间
为区间 上的“
上的“ 阶
阶 函数”若函数
函数”若函数 为区间
为区间 上的“
上的“ 阶
阶 函数”,则
函数”,则 的值为( )
的值为( )
| A.4 | B.3 | C.2 | D.1 |
对任意的 、
、 ,定义:
,定义: =
= ;
; =
= .则下列各式中
.则下列各式中
恒成立的个数为( )
①
②
③
④
| A.1 | B.2 | C.3 | D.4 |
在平面直角坐标系中,若两点 满足条件:①
满足条件:① 两点都在函数
两点都在函数 的图象上;②
的图象上;② 两点关于坐标原点对称。则对称点
两点关于坐标原点对称。则对称点 是函数
是函数 的一对“友好点对”。点
的一对“友好点对”。点 和
和 看作是同一对“友好点对”。那么函数
看作是同一对“友好点对”。那么函数 的“友好点对”有( )
的“友好点对”有( )
A. 对 对 |
B. 对 对 |
C. 对 对 |
D. 对 对 |
德国著名数学家狄利克雷在数学领域成就卓著,以其名命名的函数 被称为狄利克雷函数,则关于函数f(x)有如下四个命题:
被称为狄利克雷函数,则关于函数f(x)有如下四个命题:
① ;
;
②函数f(x)是偶函数;
③任何一个不为零的有理数T,f(x+T)=f(x)对任意的 恒成立;
恒成立;
④存在三个点 ,使得△ABC为等边三角形.
,使得△ABC为等边三角形.
其中证明题的个数是
| A.1 | B.2 | C.3 | D.4 |
设 的定义域为
的定义域为 ,若
,若 满足下面两个条件,则称
满足下面两个条件,则称 为闭函数.①
为闭函数.① 在
在 内是单调函数;②存在
内是单调函数;②存在 ,使
,使 在
在 上的值域为
上的值域为 ,如果
,如果 为闭函数,那么
为闭函数,那么 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
设集合 是
是 的两个非空子集,如果存在一个从
的两个非空子集,如果存在一个从 到
到 的函数
的函数 满足:
满足:  对任意
对任意 当
当 时,恒有
时,恒有 ,那么称这两个集合“保序同构”.以下集合对不是“保序同构”的是( )
,那么称这两个集合“保序同构”.以下集合对不是“保序同构”的是( )
A. |
B. |
C. |
D. |
定义符号函数  ,则下列结论中错误的是
,则下列结论中错误的是
A. |
B. |
C. |
D. |