已知函数f(x)=sinx+cosx.
(1)若f(x)=2f(﹣x),求 的值;
的值;
(2)求函数F(x)=f(x)•f(﹣x)+f2(x)的最大值和单调递增区间.
已知sinx=2cosx,则sin2x+1=( )
A. |
B. |
C. |
D. |
设当x=θ时,函数f(x)=sin x-2cos x取得最大值,则cos θ=________.
已知f(x)=sin2 ,若a=f(lg 5),b=f
,若a=f(lg 5),b=f ( ).
( ).
| A.a+b=0 | B.a-b=0 | C.a+b=1 | D.a-b=1 |
关于函数f(x)=4sin(2x+ ),(x∈R)有下列命题:
),(x∈R)有下列命题:
①y=f(x)是以2π为最小正周期的周期函数;
②y=f(x)可改写为y=4cos(2x﹣ );
);
③y=f(x)的图象关于点(﹣ ,0)对称;
,0)对称;
④y=f(x)的图象关于直线x= 对称;
对称;
其中正确的序号为 .
(本小题满分12分)(1)已知角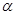 的顶点在原点,始边与
的顶点在原点,始边与 轴的非负半轴重合,终边经过点
轴的非负半轴重合,终边经过点 ,求
,求 的值.
的值.
(2)在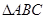 中,
中, ,求
,求 的值.
的值.
已知函数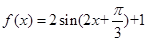 .
.
(Ⅰ)当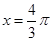 时,求
时,求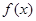 值;
值;
(Ⅱ)若存在区间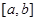 (
(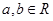 且
且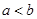 ),使得
),使得 在
在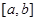 上至少含有6个零
上至少含有6个零
点,在满足上述条件的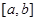 中,求
中,求 的最小值.
的最小值.
已知向量 与
与 ,其中
,其中 .
.
(1)问向量 能平行吗?请说明理由;
能平行吗?请说明理由;
(2)若 ,求
,求 和
和 的值;
的值;
(3)在(2)的条件下,若
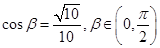 ,求
,求 的值.
的值.
求值:sin(-1 200°)·cos 1 290°+cos(-1 020°)·sin(-1 050°)+tan 945°.