2014年高考数学(理)二轮复习专题能力测评3练习卷
已知f(x)=sin2 ,若a=f(lg 5),b=f
,若a=f(lg 5),b=f ( ).
( ).
| A.a+b=0 | B.a-b=0 | C.a+b=1 | D.a-b=1 |
来源:2014年高考数学(理)二轮复习专题能力测评3练习卷
设△ABC的内角A,B,C所对边的长分别为a,b,c.若b+c=2a,3sin A=5sin B,则角C= ( ).
A. |
B. |
C. |
D. |
来源:2014年高考数学(理)二轮复习专题能力测评3练习卷
在△ABC中,若sin2A+sin2B<sin2C,则△ABC的形状是( ).
| A.锐角三角形 | B.直角三角形 | C.钝角三角形 | D.不能确定 |
来源:2014年高考数学(理)二轮复习专题能力测评3练习卷
设函数f(x)=sin(ωx+φ)+cos(ωx+φ)  的最小正周期为π,且f(-x)=f(x),则( ).
的最小正周期为π,且f(-x)=f(x),则( ).
A.f(x)在 单调递减 单调递减 |
B.f(x)在 单调递减 单调递减 |
C.f(x)在 单调递增 单调递增 |
D.f(x)在 单调递增 单调递增 |
来源:2014年高考数学(理)二轮复习专题能力测评3练习卷
将函数f(x)=sin(2x+θ)(- <θ<
<θ< )的图象向右平移φ(φ>0)个单位长度后得到函数g(x)的图象,若f(x),g(x)的图象都经过点P(0,
)的图象向右平移φ(φ>0)个单位长度后得到函数g(x)的图象,若f(x),g(x)的图象都经过点P(0, ),则φ的值可以是( ).
),则φ的值可以是( ).
A. |
B. |
C. |
D. |
来源:2014年高考数学(理)二轮复习专题能力测评3练习卷
函数f(x)=sin x-cos  的值域为( ).
的值域为( ).
| A.[-2,2] | B. |
C.[-1,1] | D. |
来源:2014年高考数学(理)二轮复习专题能力测评3练习卷
在△ABC中,内角A,B,C所对的边分别是a,b,c.已知8b=5c,C=2B,则cos C=( ).
A.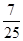 |
B.-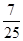 |
C.±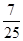 |
D.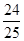 |
来源:2014年高考数学(理)二轮复习专题能力测评3练习卷
在△ABC中,内角A,B,C的对边分别为a,b,c.若asin Bcos C+csin Bcos A=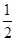 b,且a>b,则∠B=( ).
b,且a>b,则∠B=( ).
A.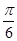 |
B.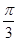 |
C. |
D.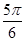 |
来源:2014年高考数学(理)二轮复习专题能力测评3练习卷
设f(x)= sin 3x+cos 3x,若对任意实数x都有|f(x)|≤a,则实数a的取值范围是________.
sin 3x+cos 3x,若对任意实数x都有|f(x)|≤a,则实数a的取值范围是________.
来源:2014年高考数学(理)二轮复习专题能力测评3练习卷
设△ABC的内角A,B,C的对边分别为a,b,c,且a=1,b=2,cos C= ,则sin B=________.
,则sin B=________.
来源:2014年高考数学(理)二轮复习专题能力测评3练习卷
已知函数f(x)=Atan(ωx+φ)(ω>0,|φ|< ),y=f(x)的部分图象如图所示,则f
),y=f(x)的部分图象如图所示,则f =________.
=________.
来源:2014年高考数学(理)二轮复习专题能力测评3练习卷
在△ABC中,∠C=90°,M是BC的中点.若sin∠BAM= ,则sin∠BAC=________.
,则sin∠BAC=________.
来源:2014年高考数学(理)二轮复习专题能力测评3练习卷
函数f(x)=Asin  +1(A>0,ω>0)的最大值为3,其图象相邻两条对称轴之间的距离为
+1(A>0,ω>0)的最大值为3,其图象相邻两条对称轴之间的距离为 .
.
(1)求函数f(x)的解析式;
(2)设α∈ ,f
,f =2,求α的值.
=2,求α的值.
来源:2014年高考数学(理)二轮复习专题能力测评3练习卷
 图象的一条对称轴是( ).
图象的一条对称轴是( ).

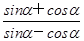 =
=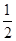 ,则tan2α=( ).
,则tan2α=( ).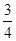
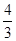
 ,∠B=2∠A.
,∠B=2∠A. cos
cos ,x∈R
,x∈R 的值;
的值; ,θ∈
,θ∈ ,求f
,求f .
. ,b=5,求sin Bsin C的值.
,b=5,求sin Bsin C的值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号