在 轴的正方向上,从左向右依次取点列
轴的正方向上,从左向右依次取点列  ,以及在第一象限内的抛物线
,以及在第一象限内的抛物线 上从左向右依次取点列
上从左向右依次取点列 ,使
,使 (
( )都是等边三角形,其中
)都是等边三角形,其中 是坐标原点,则第2005个等边三角形的边长是 .
是坐标原点,则第2005个等边三角形的边长是 .
对于自然数数组 ,如下定义该数组的极差:三个数的最大值与最小值的差.如果
,如下定义该数组的极差:三个数的最大值与最小值的差.如果 的极差
的极差 ,可实施如下操作
,可实施如下操作 :若
:若 中最大的数唯一,则把最大数减2,其余两个数各增加1;若
中最大的数唯一,则把最大数减2,其余两个数各增加1;若 中最大的数有两个,则把最大数各减1,第三个数加2,此为一次操作,操作结果记为
中最大的数有两个,则把最大数各减1,第三个数加2,此为一次操作,操作结果记为 ,其级差为
,其级差为 .若
.若 ,则继续对
,则继续对 实施操作
实施操作 ,…,实施
,…,实施 次操作后的结果记为
次操作后的结果记为 ,其极差记为
,其极差记为 .例如:
.例如: ,
, .
.
(1)若 ,求
,求 和
和 的值;
的值;
(2)已知 的极差为
的极差为 且
且 ,若
,若 时,恒有
时,恒有 ,求
,求 的所有可能取值;
的所有可能取值;
(3)若 是以4为公比的正整数等比数列中的任意三项,求证:存在
是以4为公比的正整数等比数列中的任意三项,求证:存在 满足
满足 .
.
给出下列四个命题:
① 因为 ,所以
,所以 ;
;
② 由 两边同除
两边同除 ,可得
,可得 ;
;
③ 数列1,4,7,10,…, 的一个通项公式是
的一个通项公式是 ;
;
④ 演绎推理是由一般到特殊的推理,类比推理是由特殊到特殊的推理.
其中正确命题的个数有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
已知数列{an}的通项公式为an= (-1)n n,则a4=_____.
已知数列 ,且通项公式分别为
,且通项公式分别为 ,现抽出数列
,现抽出数列 中所有相同的项并按从小到大的顺序排列成一个新的数列
中所有相同的项并按从小到大的顺序排列成一个新的数列 ,则可以推断
,则可以推断 (用
(用 表示(
表示( )).
)).
如果存在常数a使得数列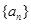 满足:若x是数列
满足:若x是数列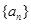 中的任意一项,则
中的任意一项,则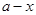 也是数列
也是数列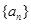 中的一项,称数列
中的一项,称数列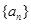 为“兑换数列”,常数a是它的“兑换系数”.如数列:1,3,6,8是以9为“兑换系数”的“兑换数列”.已知等差数列
为“兑换数列”,常数a是它的“兑换系数”.如数列:1,3,6,8是以9为“兑换系数”的“兑换数列”.已知等差数列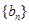 是“兑换数列”,则数列
是“兑换数列”,则数列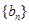 的“兑换系数”是 .
的“兑换系数”是 .
对于数列{an},a1=4,an+1=f(an)n=1,2…,则a2011等于( )
| x |
1 |
2 |
3 |
4 |
5 |
| f(x) |
5 |
4 |
3 |
1 |
2 |
A.2 B.3 C.4 D.5
设数列{an}的前n项和Sn=n2,则a8的值为( )
| A.15 | B.16 | C.49 | D.64 |
若f(x)= ,则f(1)+f(2)+f(3)…+f(2011)+f(
,则f(1)+f(2)+f(3)…+f(2011)+f( )+f(
)+f( )+…+f(
)+…+f( )=( )
)=( )
| A.2009 | B.2010 |
C.2012 | D.1 |
已知数列{an}的通项公式是an=n2+kn+2,若对于n∈N*,都有an+1>an成立,则实数的取值范围( )
| A.k>0 | B.k>﹣1 | C.k>﹣2 | D.k>﹣3 |
已知数列{an}满足an+2=an+1+an,若a1=1,a5=8,则a3=( )
| A.1 | B.2 | C.3 | D. |