给出下面四个命题,不正确的是: .
①若向量 、
、 满足
满足 ,且
,且 与
与 的夹角为
的夹角为 ,则
,则 在
在 上的投影等于
上的投影等于 ;
;
②若等比数列 的前
的前 项和为
项和为 ,则
,则 、
、 、
、 也成等比数列;
也成等比数列;
③常数列既是等差数列,又是等比数列;
④若向量 与
与 共线,则存在唯一实数
共线,则存在唯一实数 ,使得
,使得 成立。
成立。
⑤在正项等比数列 中,若
中,若 ,则
,则
已知数列 中,
中, ,则数列
,则数列 通项公式
通项公式 =______________.
=______________.
已知数列 满足
满足
(1)分别求 的值。
的值。
(2)猜想 的通项公式
的通项公式 ,并用数学归纳法证明。
,并用数学归纳法证明。
观察如图三角形数阵,则
(1)若记第n行的第m个数为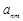 ,则
,则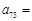 .
.
(2)第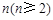 行的第2个数是 .
行的第2个数是 .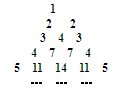
对于各项均为整数的数列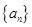 ,如果
,如果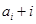 (
(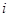 =1,2,3,…)为完全平方数,则称数列
=1,2,3,…)为完全平方数,则称数列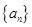 具有“
具有“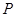 性质”.不论数列
性质”.不论数列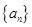 是否具有“
是否具有“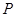 性质”,如果存在与
性质”,如果存在与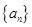 不是同一数列的
不是同一数列的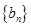 ,且
,且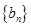 同时满足下面两个条件:①
同时满足下面两个条件:① 是
是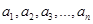 的一个排列;②数列
的一个排列;②数列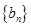 具有“
具有“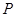 性质”,则称数列
性质”,则称数列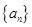 具有“变换
具有“变换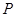 性质”.下面三个数列:①数列
性质”.下面三个数列:①数列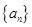 的前
的前 项和
项和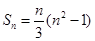 ;②数列1,2,3,4,5;③1,2,3,…,11.具有“
;②数列1,2,3,4,5;③1,2,3,…,11.具有“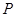 性质”的为 ;具有“变换
性质”的为 ;具有“变换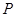 性质”的为 .
性质”的为 .
设各项都是正整数的无穷数列 满足:对任意
满足:对任意 ,有
,有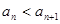 .记
.记 .
.
(1)若数列 是首项
是首项 ,公比
,公比 的等比数列,求数列
的等比数列,求数列 的通项公式;
的通项公式;
(2)若 ,证明:
,证明: ;
;
(3)若数列 的首项
的首项 ,
, ,
, 是公差为1的等差数列.记
是公差为1的等差数列.记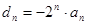 ,
, ,问:使
,问:使 成立的最小正整数
成立的最小正整数 是否存在?并说明理由.
是否存在?并说明理由.
已知正项数列 满足:
满足: ,数列
,数列 的前
的前 项和为
项和为 ,且满足
,且满足 ,
, .
.
(1)求数列 和
和 的通项公式;
的通项公式;
(2)设 ,数列
,数列 的前
的前 项和为
项和为 ,求证:
,求证: .
.
已知正项数列 满足:
满足: ,数列
,数列 的前
的前 项和为
项和为 ,且满足
,且满足 ,
, .
.
(1)求数列 和
和 的通项公式;
的通项公式;
(2)设 ,数列
,数列 的前
的前 项和为
项和为 ,求证:
,求证: .
.