高中数学一阶、二阶线性常系数递归数列的通项公式填空题

给出下面四个命题，不正确的是：               ．
①若向量、满足，且与的夹角为，则在上的投影等于；
②若等比数列的前项和为，则、、也成等比数列；
③常数列既是等差数列，又是等比数列；
④若向量与共线，则存在唯一实数，使得成立。
⑤在正项等比数列中，若，则

观察如图三角形数阵，则
（1）若记第n行的第m个数为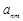，则     ．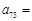
（2）第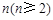行的第2个数是     ．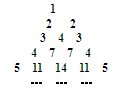

对于各项均为整数的数列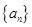，如果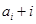(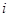=1，2，3，…)为完全平方数，则称数列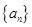具有“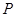性质”．不论数列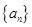是否具有“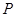性质”，如果存在与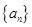不是同一数列的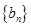，且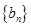同时满足下面两个条件：①是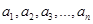的一个排列；②数列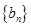具有“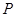性质”，则称数列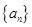具有“变换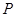性质”．下面三个数列：①数列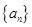的前项和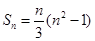；②数列1，2，3，4，5；③1，2，3，…，11.具有“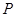性质”的为         ；具有“变换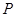性质”的为         .

给出下列五个命题：
①中，是成立的充要条件；
②当时，有；
③已知是等差数列的前n项和，若，则；
④若函数为R上的奇函数，则函数的图象一定关于点成中心对称.
⑤函数有最大值为，有最小值为0。
其中所有正确命题的序号为          ．

已知数列{a_n}中，a₁＝1，(n＋1)a_n＋1＝na_n(n∈N^*)，则该数列的通项公式a_n＝________．

已知在平面直角坐标系中有一个点列：，……，．若点到点的变化关系为：，则等于      ．

若数列{a_n}满足a₁＝2且a_n＋a_n－1＝2ⁿ＋2^n－1，S_n为数列{a_n}的前n项和，则log₂(S_{2 012}＋2)＝________.

已知数列的通项公式为，前项和为，若对任意的正整数，不等式恒成立，则常数所能取得的最大整数为           .

已知数列{a_n}中,a₁=,a_n+1=1-(n≥2),则a₁₆=　　　　　　.

已知数列{a_n}满足:a₁=m(m为正整数),a_n+1=若a₆=1,则m所有可能的值为　　　.

数列-,,-,,…的一个通项公式可以是　　　.

如图是网络工作者经常用来解释网络运作的蛇形模型：数字1出现在第1行；数字2,3出现在第2行；数字6,5,4(从左至右)出现在第3行；数字7,8,9,10出现在第4行，依次类推，则(1)按网络运作顺序第n行第1个数字(如第2行第1个数字为2，第3行第1个数字为4，…)是__________；(2)第63行从左至右的第4个数字应是__________．

第30届奥运会在伦敦举行．设数列a_n＝log_n＋1(n＋2)(n∈N^*)，定义使a₁·a₂·a₃…a_k为整数的实数k为奥运吉祥数，则在区间[1,2 012]内的所有奥运吉祥数之和为________．

设S_n为数列{a_n}的前n项和，S_n＝(－1)ⁿa_n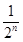－，n∈N^*，则S₁＋S₂＋S₃＋…＋S₁₀₀＝________.

对于正项数列{a_n}，定义H_n＝为{a_n}的“光阴”值，现知某数列的“光阴”值为H_n＝，则数列{a_n}的通项公式为________．