高中数学不定方程和方程组填空题

设函数若，则函数的零点个数有              个.

若关于的一元二次方程的两根均大于5，则实数的取值范围是          ．

已知函数，下列关于函数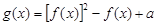（其中a为常数）的叙述中:
①a>0，函数g（x）至少有4个零点;
②当a＝0时，函数g（x）有5个不同零点;
③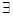a∈R，使得函数g（x）有6个不同零点;
④函数g（x）有8个不同零点的充要条件是0<a<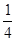.其中真命题有________.（把你认为的真命题的序号都填上）

已知,若关于的方程有实根,则的取值范围是       .

已知函数是定义在上的奇函数，当时，给出以下命题：
①当时，；    ②函数有五个零点；
③对恒成立.
④若关于的方程有解，则实数的取值范围是；
其中，正确命题的序号是                   .

方程有两个根，则的范围为         

已知函数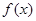的图象是连续不断的，观察下表：

x	-2	-1	0	1	2
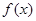	-6	3	-3	-2	1

 
函数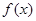在区间[-2,2]上的零点至少有_____个.

求“方程的解”有如下解题思路：设，则在上单调递减，且，所以原方程有唯一解．类比上述解题思路，方程的解集为_      __        ．

（函数的零点个数是.

要制作一个容器为4，高为的无盖长方形容器，已知该容器的底面造价是每平方米20元，侧面造价是每平方米10元，则该容器的最低总造价是（单位：元）

已知函数 $f\left(x\right)=\left|x^2+3x\right|$， $x\in R$．若方程 $f\left(x\right)-a\left|x-1\right|=0$恰有4个互异的实数根，则实数 $a$的取值范围为．

若关于的方程在区间上有两个不同的实数解，则实数的取值范围为 ．

设函数，，则函数的零点有个.

已知0<a<1，k≠0，函数f(x)＝，若函数g(x)＝f(x)－k有两个零点，则实数k的取值范围是________．

用二分法研究函数f(x)＝x³＋3x－1的零点时，第一次经计算f(0)<0，f(0.5)>0可得其中一个零点x₀∈________，第二次应计算________．