高中数学不定方程和方程组填空题

已知直线与曲线恰有四个不同的交点，则实数k的取值范围为     ．

函数f（x）＝2^x－5的零点所在区间为[m，m＋1]（m∈N），则m＝         ．

设，已知，若关于的方程恰有三个互不相等的实根，则的取值范围是         。 

已知函数，关于x的函数有8个不同的零点，则实数b的范围为        ．

定义在上的函数满足：①当时，；②．设关于的函数的零点从小到大依次为．若，则   ________ ；若，则________________．

若关于的一元二次方程的两根均大于5，则实数的取值范围是           ．

设常数使方程 在闭区间上恰有三个解，则     ．

已知f（x）为定义在R上的偶函数，当x≥0时，有f（x+1）=﹣f（x），且当x∈[0，1）时，f（x）=log₂（x+1），给出下列命题：
①f（2013）+f（﹣2014）的值为0；
②函数f（x）在定义域上为周期是2的周期函数；
③直线y=x与函数f（x）的图象有1个交点；
④函数f（x）的值域为（﹣1，1）．
其中正确的命题序号有          ．

已知函数有两个极值点，若，则关于的方程的不同实根个数为    ．

已知，则        ．

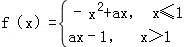若∃x₁，x₂∈R，x₁≠x₂，使得f（x₁）=f（x₂）成立，则实数a的取值范围是      ．

已知函数，，则函数的零点个数为             ．

函数f（x）=ax³﹣3x²+1，若f（x）=0存在唯一正实数根x₀，则a取值范围是       ．

己知函数f（x）=|lnx|，，则方程|f（x）+g（x）| =1实根的个数为      个．

某同学在借助计算器求“方程的近似解（精确到0．1）”时，设，算得；在以下过程中，他用“二分法”又取了4个的值，计算了其函数值的正负，并得出判断：方程的近似解是．
那么他又取的的4个值分别依次是                                     ．