高中数学不定方程和方程组填空题

定义，若，且直线与的图象有3个交点，横坐标分别为，则的最大值为          .

若函数有两个零点，则实数b的取值范围是            ．

已知函数，若关于的方程有两个不同的实根，则实数的取值范围是              ．

若内有两个不同的零点，则的取值范围是     ．

已知函数，，若有两个不相等的实根，则实 数的取值范围是____________. 

定义，若关于的方程恰有二个不同的实根，则的值为    ．

已知函数有零点，则的取值范围是        .

若对于定义在R上的函数 ,其图象是连续不断的，且存在常数使得对任意实数都成立，则称 是一个“—伴随函数”．有下列关于 “—伴随函数”的结论：
①是常数函数中唯一个“—伴随函数”；
②不是“—伴随函数”；
③是一个“—伴随函数”；
④“—伴随函数”至少有一个零点．
其中不正确的序号是_________（填上所有不正确的结论序号）．

已知，则        ．

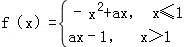若∃x₁，x₂∈R，x₁≠x₂，使得f（x₁）=f（x₂）成立，则实数a的取值范围是      ．

已知函数，，则函数的零点个数为             ．

函数f（x）=ax³﹣3x²+1，若f（x）=0存在唯一正实数根x₀，则a取值范围是       ．

己知函数f（x）=|lnx|，，则方程|f（x）+g（x）| =1实根的个数为      个．

某同学在借助计算器求“方程的近似解（精确到0．1）”时，设，算得；在以下过程中，他用“二分法”又取了4个的值，计算了其函数值的正负，并得出判断：方程的近似解是．
那么他又取的的4个值分别依次是                                     ．

若实数满足，则的取值范围是____________________.