以下有关命题的说法错误的是( )
A.命题“若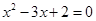 ,则 ,则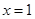 ”的逆否命题为“若 ”的逆否命题为“若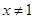 ,则 ,则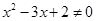 ” ” |
B.“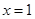 ”是“ ”是“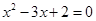 ”的充分不必要条件 ”的充分不必要条件 |
C.若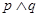 为假命题,则 为假命题,则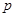 、 、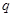 均为假命题 均为假命题 |
D.对于命题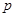 : :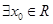 ,使得 ,使得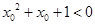 ,则 ,则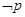 : :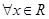 ,则 ,则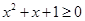 |
下列有关命题的说法正确的是 ( ).
A.命题“若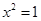 ,则 ,则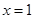 ”的否命题为:“若 ”的否命题为:“若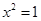 ,则 ,则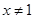 ”. ”. |
B.“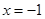 ” 是“ ” 是“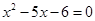 ”的必要不充分条件. ”的必要不充分条件. |
C.命题“若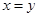 ,则 ,则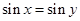 ”的逆否命题为真命题. ”的逆否命题为真命题. |
D.命题“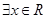 使得 使得 ”的否定是:“ ”的否定是:“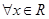 均有 均有 ”. ”. |
.命题“存在 ”的否定是
”的否定是
A.不存在 <0 <0 |
B.存在 <0 <0 |
C.对任意的 |
D.对任意的 <0 <0 |
下列命题中的说法正确的是
A.若向量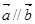 ,则存在唯一的实数 ,则存在唯一的实数 使得 使得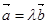 ; ; |
B.命题“若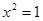 ,则 ,则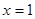 ”的否命题为“若 ”的否命题为“若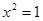 ,则 ,则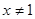 ”; ”; |
C.命题“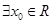 ,使得 ,使得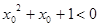 ”的否定是:“ ”的否定是:“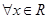 ,均有 ,均有 ”; ”; |
D.“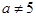 且 且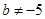 ”是“ ”是“ ”的不充分也不必要条件; ”的不充分也不必要条件; |
下列结论:
①若命题 ;命题
;命题 ,
,
则命题“ ”是假命题;
”是假命题;
②某校在一次月考中约有1000人参加考试,数学考试的成绩 ~
~
 ,统计结果显示数字考试成绩在70分到110分之间的人数约为总人数的
,统计结果显示数字考试成绩在70分到110分之间的人数约为总人数的 则此次月考中数学考试成绩不低于110分的学生约有200人;
则此次月考中数学考试成绩不低于110分的学生约有200人;
③在线性回归分析中,残差的平方和越小,说明模型的拟合效果越好;
④对分类变量X与Y,它们的随机变量K2的观测值为k,若k越大,则“X与Y有关
系”的把握程度越大,其中结论正确的个数为 ( )
| A.4 | B.3 | C.2 | D.1 |
已知命题p:∃x∈R,x2+1<2x;命题q:若mx2-mx-1<0恒成立,则-4<m≤0,那么( )
A.“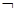 p”是假命题 p”是假命题 |
B.“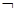 q”是真命题 q”是真命题 |
| C.“p∧q”为真命题 | D.“p∨q”为真命题 |
用反证法 证明命题:“若整系数一元二次方程
证明命题:“若整系数一元二次方程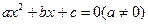 有有理根,那么
有有理根,那么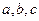 中至少有一个是偶数时,下列假设中正确的是
中至少有一个是偶数时,下列假设中正确的是
A.假设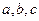 都是偶数 都是偶数 |
B.假设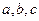 都不是偶数 都不是偶数 |
C.假设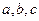 至多有一个是偶数 至多有一个是偶数 |
D.假设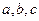 至多有两个是偶数 至多有两个是偶数 |
下列命题中,真命题是( )
A.对于任意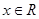 , ,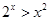 ; ; |
B.若“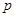 且 且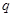 ”为假命题,则 ”为假命题,则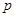 , ,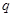 均为假命题; 均为假命题; |
C.“平面向量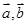 的夹角是钝角”的充分不必要条件是“ 的夹角是钝角”的充分不必要条件是“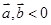 ”; ”; |
D.存在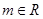 ,使 ,使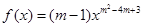 是幂函数,且在 是幂函数,且在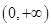 上是递减的. 上是递减的. |
给出下列四个命题:
(1)命题“若 ,则tanα=1”的逆否命题为假命题;
,则tanα=1”的逆否命题为假命题;
(2)命题p:∀x∈R,sinx≤1.则¬p:∃x0∈R,使sinx0>1;
(3)“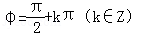 ”是“函数y=sin(2x+ϕ)为偶函数”的充要条件;
”是“函数y=sin(2x+ϕ)为偶函数”的充要条件;
(4)命题p:“∃x0∈R,使 ”;命题q:“若sinα>sinβ,则α>β”,那么(¬p)∧q为真命题.
”;命题q:“若sinα>sinβ,则α>β”,那么(¬p)∧q为真命题.
其中正确的个数是( )
| A.1 | B.2 | C.3 | D.4 |
给出下列命题:
①若给定命题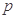 :
: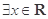 ,使得
,使得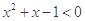 ,则
,则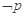 :
: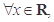 均有
均有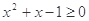 ;
;
②若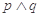 为假命题,则
为假命题,则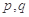 均为假命题;
均为假命题;
③命题“若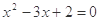 ,则
,则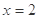 ”的否命题为“若
”的否命题为“若 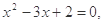 则
则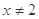
其中正确的命题序号是( )
| A.① | B.①② | C.①③ | D.②③ |
已知函数f(x)=sin x- x(x∈[0,π]),那么下列结论正确的是 ( ).
x(x∈[0,π]),那么下列结论正确的是 ( ).
A.f(x)在 上是增函数 上是增函数 |
B.f(x)在 上是减函数 上是减函数 |
C.∃x∈ , , |
D.∀x∈ , , 。 。 |