已知 ,函数
,函数 的零点分别为
的零点分别为 ,函数
,函数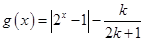 的零点分别为
的零点分别为 ,则
,则 的最小值为( )
的最小值为( )
A. |
B.2 | C. |
D.1 |
已知函数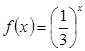 ,
, ,函数
,函数 的最小值为
的最小值为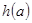 .
.
(1)求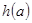 ;
;
(2)是否存在实数 、
、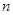 同时满足以下条件:
同时满足以下条件:
①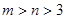 ;
;
②当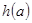 的定义域为
的定义域为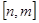 时,值域为
时,值域为 .若存在,求出
.若存在,求出 、
、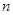 的值;若不存在,说明理由
的值;若不存在,说明理由
已知直线y=mx与函数 的图象恰好有3个不同的公共点,则实数m的取值范围是( )
的图象恰好有3个不同的公共点,则实数m的取值范围是( )
A.( ,4) ,4) |
B.( ,+∞) ,+∞) |
C.( ,5) ,5) |
D.( , , ) ) |
设函数 ,若对任意给定的
,若对任意给定的 ,都存在唯一的
,都存在唯一的 ,满足
,满足 ,则正实数
,则正实数 的最小值是( )
的最小值是( )
A. |
B. |
C.2 | D.4 |
已知定义在 上的函数 ( 为实数)为偶函数,记 ,则 的大小关系为()
| A. | B. | C. | D. |
命题p:关于x的不等式x2+2ax+4>0,对一切x∈R恒成立,命题q:指数函数f(x)=(3﹣2a)x是增函数,若p∨q为真,p∧q为假,求实数a的取值范围.
设f(x)=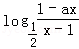 为奇函数,a为常数.
为奇函数,a为常数.
(1)求a的值;
(2)判断f(x)在区间(1,+∞)上的单调性,并证明你的结论;
(3)若对于区间(3,4)上的每一个x的值,不等式f(x)>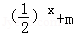 恒成立,
恒成立,
求实数m的取值范围.