高中数学随机思想的发展试题

一批产品需要进行质量检验，质检部门规定的检验方案是：先从这批产品中任取3件作检验，若3件产品都是合格品，则通过检验；若有2件产品是合格品，则再从这批产品中任取1件作检验，这1件产品是合格品才能通过检验；若少于2件合格品，则不能通过检验，也不再抽检. 假设这批产品的合格率为80%，且各件产品是否为合格品相互独立.
(1)求这批产品通过检验的概率；
(2)已知每件产品检验费为125元，并且所抽取的产品都要检验，记这批产品的检验费为元，求的概率分布及数学期望.

如图，一半径为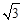的圆形靶内有一个半径为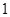的同心圆，将大圆分成两
部分，小圆内部区域记为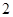环，圆环区域记为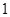环，某同学向该靶投掷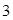枚飞镖，每次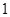枚. 假设他每次必
定会中靶，且投中靶内各点是随机的.
（1）求该同学在一次投掷中获得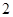环的概率；
（2）设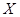表示该同学在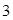次投掷中获得的环数，求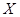的分布列及数学期望.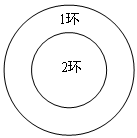

在某校教师趣味投篮比赛中,比赛规则是: 每场投6个球，至少投进4个球且最后2个球都投进者获奖；否则不获奖. 已知教师甲投进每个球的概率都是．
（1）记教师甲在每场的6次投球中投进球的个数为X，求X的分布列及数学期望；
（2）求教师甲在一场比赛中获奖的概率；
（3）已知教师乙在某场比赛中，6个球中恰好投进了4个球，求教师乙在这场比赛中获奖的概率；教师乙在这场比赛中获奖的概率与教师甲在一场比赛中获奖的概率相等吗？

某学校组织了一次安全知识竞赛，现随机抽取20名学生的测试成绩，如下表所示（不低于90分的测试成绩称为“优秀成绩”）：

79	90	82	80	84	95	79	86	89	91
97	86	79	78	86	77	87	89	83	85

 
（1）若从这20人中随机选取3人，求至多有1人是“优秀成绩”的概率；
（2）以这20人的样本数据来估计整个学校的总体数据，若从该校全体学生中（人数很多）任选3人，记表示抽到“优秀成绩”学生的人数，求的分布列及数学期望.

为了解某校学生的视力情况，现采用随机抽样的方式从该校的A，B两班中各抽5名学生进行视力检测．检测的数据如下：
A班5名学生的视力检测结果：4.3，5.1，4.6，4.1，4.9.
B班5名学生的视力检测结果：5.1，4.9，4.0，4.0，4.5.
（1）分别计算两组数据的平均数，从计算结果看，哪个班的学生视力较好？
（2）由数据判断哪个班的5名学生视力方差较大？（结论不要求证明）
（3） 现从A班的上述5名学生中随机选取3名学生，用X表示其中视力大于4.6的人数，求X的分布列和数学期望.

某商场举行的"三色球"购物摸奖活动规定：在一次摸奖中，摸奖者先从装有3个红球与4个白球的袋中任意摸出3个球，再从装有1个蓝球与2个白球的袋中任意摸出1个球，根据摸出4个球中红球与蓝球的个数，设一、二、三等奖如下：

奖级	摸出红、蓝球个数	获奖金额
一等奖	3红1蓝	200元
二等奖	3红0蓝	50元
三等奖	2红1蓝	10元

其余情况无奖且每次摸奖最多只能获得一个奖级．
（1）求一次摸奖恰好摸到1个红球的概率；
（2）求摸奖者在一次摸奖中获奖金额的分布列与期望．

某毕业生参加人才招聘会，分别向甲、乙、丙三个公司投递了个人简历，假定该毕业生得到甲公司面试的概率为 $\frac{2}{3}$，得到乙、丙公司面试的概率均为 $P$，且三个公司是否让其面试是相互独立的．记 $X$为该毕业生得到面试的公司个数．若 $P(X=0)=\frac{1}{12}$，则随机变量 $X$的数学期望 $E\left(X\right)=$．

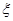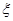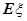小李练习射击，每次击中目标的概率为，用表示小李射击次击中目标的次数，则的均值与方差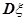的值分别是______________________．

(14分)某工厂在试验阶段大量生产一种零件，这种零件有、两项技术指标需要检测，设各项技术指标达标与否互不影响.若仅有A项技术指标达标的概率为，A、B两项技术指标都不达标的概率为．按质量检验规定：两项技术指标都达标的零件为合格品．
（1）求一个零件经过检测为合格品的概率？
（2）若任意抽取该种零件4个，设表示其中合格品的个数，求的分布列及数学期望．

假设某班级教室共有4扇窗户，在每天上午第三节课上课预备铃声响起时，每扇窗户或被敞开或被关闭，且概率均为，记此时教室里敞开的窗户个数为X．
(1)求X的分布及数学期望；
(2)若此时教室里有两扇或两扇以上的窗户被关闭，班长就会将关闭的窗户全部敞开，否则维持原状不变．记每天上午第三节课上课时该教室里敞开的窗户个数为Y，求Y的数学期望．

设袋子中装有个红球，个黄球，个蓝球，且规定：取出一个红球得1分，取出一个黄球2分，取出蓝球得3分．
（1）当=3，=2，=1时，从该袋子中任取（有放回，且每球取到的机会均等）2个球，记随机变量为取出此2球所得分数之和．，求分布列；
（2）从该袋子中任取（且每球取到的机会均等）1个球，记随机变量为取出此球所得分数．若，求：：．

如图是某市3月1日至14日的空气质量指数趋势图．空气质量指数小于100表示空气质量优良，空气质量指数大于200表示空气重度污染．某人随机选择3月1日至3月13日中的某一天到达该市，并停留2天．
(1)求此人到达当日空气质量优良的概率；
(2)求此人在该市停留期间只有1天空气重度污染的概率；
(3)由图判断从哪天开始连续三天的空气质量指数方差最大？(结论不要求证明)

为调查某社区居民的业余生活状况，研究这一社区居民在20：00－22：00时间段的休闲方式与性别的关系，随机调查了该社区80人，得到下面的数据表：

休闲方式 性别	看电视	看书	合计
男	10	50	60
女	10	10	20
合计	20	60	80

 
(1)将此样本的频率估计为总体的概率，随机调查3名在该社区的男性，设调查的3人在这一时间段以看书为休闲方式的人数为随机变量X，求X的分布列和数学期望；
(2)根据以上数据，我们能否在犯错误的概率不超过0．01的前提下，认为“在20：00－22：00时间段居民的休闲方式与性别有关系”？
参考公式：K²＝，其中n＝a＋b＋c＋d．
参考数据：

P(K^2≥k0)	0．15	0．10	0．05	0．025	0．010
k0	2．072	2．706	3．841	5．024	6．635

 

下图是某市3月1日至14日空气质量指数趋势图，空气质量指数小于1 00表示空气质量优良，空气质量指数大于200表示空气重度污染，某人随机选择3月1曰至3月1 3日中某一天到达该市，并停留2天．

(l)求此人到达当日空气重度污染的概率；
(2)设X是此人停留期间空气质量优良的天数，求X的分布列与数学期望。

某中学有A、B、C、D、E五名同学在高三“一检”中的名次依次为1，2，3，4，5名，“二检”中的前5名依然是这五名同学.
（1）求恰好有两名同学排名不变的概率；
（2）如果设同学排名不变的同学人数为，求的分布列和数学期望．