2011年3月20日，第19个世界水日，主题是：“城市水资源管理”；2011年“六·五”世界环境日中国主题：“共建生态文明，共享绿色未来”．活动组织者为调查市民对活动主题的了解情况，随机对10～60岁的人群抽查了
人，调查的每个人都同时回答了两个问题，统计结果如下：
（Ⅰ）若以表中的频率近似看作各年龄段回答活动主题正确的概率，规定回答正确世界环境日中国主题的得20元奖励，回答正确世界水日主题的得30元奖励．组织者随机请一个家庭中的两名成员（大人42岁，孩子16岁）回答这两个主题，两个主题能否回答正确均无影响，分别写出这个家庭两个成员获得奖励的分布列并求该家庭获得奖励的期望；
（Ⅱ）求该家庭获得奖励为50元的概率．
有关部门要了解甲型H1N1流感预防知识在学校的普及情况，命制了一份有10道题的问卷到各学校做问卷调查．某中学A，B两个班各被随机抽取5名学生接受问卷调查，A班5名学生得分为：5、8、9、9、9；B班5名学生得分为：6，7，8，9，10．
（1）请你估计A，B两个班中哪个班的问卷得分要稳定一些；
（2）如果把B班5名学生的得分看成一个总体，并用简单随机抽样方法从中抽取样本容量为2的样本，求样本平均数与总体平均数之差的绝对值不小于1的概率．
抽签方式决定出场顺序.通过预赛，选拔出甲、乙等五支队伍参加决赛.
(Ⅰ)求决赛中甲、乙两支队伍恰好排在前两位的概率；
(Ⅱ)若决赛中甲队和乙队之间间隔的队伍数记为
，求的分布列和数学期望.
(本小题满分10分)
如图A,B两点之间有6条网线并联,它们能通过的最大信息量分别为1,1,2,2,3,4.现从中任取三条网线且使每条网线通过最大的信息量.
(1)设选取的三条网线由A到B可通过的信息
总量为
时,则保证信息畅通.
求线路信息畅通的概率;
(2)求选取的三条网线可通过信息总量的数学期望.
某商场为吸引顾客消费推出一项优惠活动.活动规则如下：消费额每满100元可转动如图所示的圆盘一次，并获得相应金额的返券，假定指针等可能地停在任一位置. 若指针停在A区域返券60元；停在B区域返券30元；停在C区域不返券. 例如：消费218元，可转动圆盘2次，所获得的返券金额是两次金额之和.
（1）若某位顾客消费128元，求返券金额不低于30元的概率；
（2）若某位顾客恰好消费280元，并按规则参与了活动，他获得返券的金额记
为
（元）.求随机变量的分布列和数学期望.
（本小题满分12分）
2008年北京奥运会乒乓球比赛将产生男子单打、女子单打、男子团体、女子团体共四枚金牌，保守估计中国乒乓球男队获得每枚金牌的概率均为
，中国乒乓球女队获得每枚金牌的概率均为
.
（1）求按此估计中国乒乓球女队比中国乒乓球男队多获得一枚金牌的概率；
（2）记中国乒乓球队获得金牌的数为
，按此估计的分布列和数学期望
。
高三某学生高考成绩
与高三期间有效复习时间
（天）正相关，且回归方程是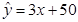
，若期望他高考达到560分，那么他的有效复习时间应不低于______天．
（本小题满分12分）某班同学利用国庆节进行社会实践，对 [25，55]岁的人群随机抽取n人进行了一次生活习惯是否符合低碳观念的调查，若生活习惯符合低碳观念的称为“低碳族”，否则称为“非低碳族”，得到如下统计表和各年龄段人数频率分布直方图：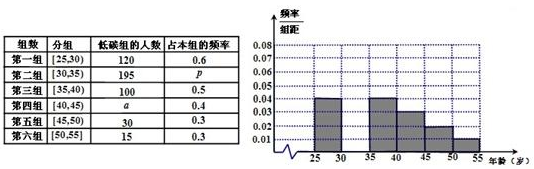
（1）补全频率分布直方图并求n、a、p的值；
（2）从[40，50）岁年龄段的“低碳族”中采用分层抽样法抽取18人参加户外低碳体验活动，其中选取3人作为领队，记选取的3名领队中年龄在[40，45）岁的人数为X，求X的分布列和期望E（X）．
（本小题满分12分）一个袋子装有大小形状完全相同的9个球，其中5个红球编号分别为l，2，3，4，5：4个白球编号分别为1，2，3，4，从袋中任意取出3个球．
（Ⅰ）求取出的3个球编号都不相同的概率；
（Ⅱ）记X为取出的3个球中编号的最大值，求X的分布列与数学期望
已知随机变量X的分布列为
| X |
1 |
2 |
3 |
| P |
0.2 |
0.4 |
0.4 |
则E(6X＋8)＝( )
A．13.2 B．21.2 C．20.2 D．22.2
2014年2月21日，《中共中央关于全面深化改革若干重大问题的决定》明确：坚持计划生育的基本国策，启动实施一方是独生子女的夫妇可生育两个孩子的政策.为了解某地区城镇居民和农村居民对“单独两孩”的看法，某媒体在该地区选择了3600人调查，就是否赞成“单独两孩”的问题，调查统计的结果如下表：
| 赞成 |
反对 |
无所谓 |
|
| 农村居民 |
2100人 |
120人 |
y人 |
| 城镇居民 |
600人 |
x人 |
z人 |
已知在全体样本中随机抽取1人，抽到持“反对”态度的人的概率为0.05.
（1）现在分层抽样的方法在所有参与调查的人中抽取360人进行问卷访谈，问应在持“无所谓”态度的人中抽取多少人？
（2）在持“反对”态度的人中，用分层抽样的方法抽取6人，按每组3人分成两组进行深入交流，求第一组中农村居民人数
的分布列和数学期望.
抽样统计甲、乙两位射击运动员的5次训练成绩（单位：环），结果如下：
则成绩较稳定（方差较小）的那位运动员成绩的方差为.
（本题12分）某位收藏爱好者鉴定一件物品时，将正品错误地鉴定为赝品的概率为
，将赝品错误地鉴定为正品的概率为
，已知一批物品共有4件，其中正品3件，赝品1件.（1）求该收藏爱好者的鉴定结果为正品2件，赝品2件的概率；（2）求该收藏爱好者的鉴定结果中正品数
的分布列及数学期望.
乒乓球单打比赛在甲、乙两名运动员间进行，比赛采用
局
胜制（即先胜局者获胜，比赛结束），假设两人在每一局比赛中获胜的可能性相同.
（Ⅰ）求甲以比
获胜的概率；
（Ⅱ）求乙获胜且比赛局数多于
局的概率；
（Ⅲ）求比赛局数的分布列.
粤公网安备 44130202000953号
