(本小题满分10分)
如图A,B两点之间有6条网线并联,它们能通过的最大信息量分别为1,1,2,2,3,4.现从中任取三条网线且使每条网线通过最大的信息量.
(1)设选取的三条网线由A到B可通过的信息
总量为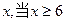
时,则保证信息畅通.
求线路信息畅通的概率;
(2)求选取的三条网线可通过信息总量的数学期望.
，解关于
的不等式
，且A.B.C成等差，求外接圆直径.
+x
,且A.B.C三点共线，求
.
数列
相关知识点
推荐套卷
(本小题满分10分)如图A,B两点之间有6条网线并联,它们能通过的最大信息量分别为1,1,2,2,3,4.现从中任取三条网线且使每条网线通过最大的信息量.
(1)设选取的三条网线由A到B可通过的信息
总量为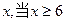时,则保证信息畅通.
求线路信息畅通的概率;
(2)求选取的三条网线可通过信息总量的数学期望.
粤公网安备 44130202000953号