高三(1)班、高三(2)班每班已选出3名学生组成代表队,进行乒乓球对抗赛. 比赛规则是:①按“单打、双打、单打”顺序进行三盘比赛;②代表队中每名队员至少参加一盘比赛,不得参加两盘单打比赛. 已知每盘比赛双方胜出的概率均为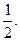
(Ⅰ)根据比赛规则,高三(1)班代表队共可排出多少种不同的出场阵容?
(Ⅱ)高三(1)班代表队连胜两盘的概率是多少?
(本小题满分14分)甲、乙两人进行乒乓球单打比赛,采用五局三胜制(即先胜三局者获冠军).对于每局比赛,甲获胜的概率为 ,乙获胜的概率为
,乙获胜的概率为 .如果将“乙获得冠军”的事件称为“爆出冷门”.试求此项赛事爆出冷门的概率.
.如果将“乙获得冠军”的事件称为“爆出冷门”.试求此项赛事爆出冷门的概率.
(本小题满分12分)已知高二年级的某6名学生,独立回答某类问题时答对的概率都是0.5,而将这6名同学平均分为甲、乙、丙3个小组后,每个小组经过两名同学讨论后再回答同类问题时答对此类问题的概率都是0.7,若各个同学或各个小组回答问题时都是相互独立的.
(Ⅰ)这6名同学平均分成3组,共有分法多少种?
(Ⅱ)若分组后,3个小组中恰有2组能答对此类问题的概率是多少?
(Ⅲ)若要求独立回答,则这6名学生中至多有4人能答对此类问题的概率是多少?
(本小题满分12分)抛一枚均匀的骰子(骰子的六面分别有数字1、2、3、4、5、6)来构造数列
(1)求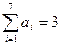 的概率;(2)若
的概率;(2)若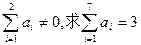 的概率.
的概率.
 某地区试行高考考试改革:在高三学年中举行5次统一测试,学生如果通过其中2次测试即可获得足够学分升上大学继续学习,不用参加其余的测试,而每个学生最多也只能参加5次测试. 假设某学生每次通过测试的概率都是
某地区试行高考考试改革:在高三学年中举行5次统一测试,学生如果通过其中2次测试即可获得足够学分升上大学继续学习,不用参加其余的测试,而每个学生最多也只能参加5次测试. 假设某学生每次通过测试的概率都是 ,每次测试通过与否互相独立. 规定:若前4次都没有通过测试,则第5次不能参加测试.
,每次测试通过与否互相独立. 规定:若前4次都没有通过测试,则第5次不能参加测试. (1)求该学生恰好经过4次测试考上大学的概率;
(1)求该学生恰好经过4次测试考上大学的概率; (2)求该学生考上大学的概率.
(2)求该学生考上大学的概率.

(本小题满分12分) 某公司是否对某一项目投资,由甲、乙、丙三位决策人投票决定.他们三人都有“同意”、“中立”、“反对”三类票各一张.投票时,每人必须且只能投一张票,每人投三类票中的任何一类票的概率都为 ,他们的投票相互没有影响.规定:若投票结果中至少有两张“同意”票,则决定对该项目投资;否则,放弃对该项目投资.(Ⅰ)求此公司决定对该项目投资的概率(Ⅱ)求此公司放弃对该项目投资且投票结果中最多有一张“中立”票的概率。
,他们的投票相互没有影响.规定:若投票结果中至少有两张“同意”票,则决定对该项目投资;否则,放弃对该项目投资.(Ⅰ)求此公司决定对该项目投资的概率(Ⅱ)求此公司放弃对该项目投资且投票结果中最多有一张“中立”票的概率。