为了解七班学生喜爱打篮球是否与性别有关，对本班50人进行了问卷调查得到了如下的列联表：
| |
喜爱打篮球 |
不喜爱打篮球 |
合计 |
| 男生 |
|
5 |
|
| 女生 |
10 |
|
|
| 合计 |
|
|
50 |
已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为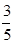
．
（1）请将上面的列联表补充完整(不用写计算过程)；
（2）能否在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关？说明你的理由；
（3）现从女生中抽取2人进一步调查，设其中喜爱打篮球的女生人数为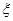
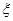，求的分布列与期望.
下面的临界值表供参考：
 |
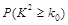0.15 |
0.10 |
0.05[ |
0.025 |
0.010 |
0.005 |
0.001 |
 |
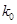2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(参考公式：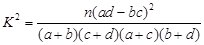
，其中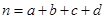
)
为考察某种药物预防禽流感的效果，进行动物家禽试验，调查了100个样本，统计结果为：服用药的共有60个样本，服用药但患病的仍有20个样本，没有服用药且未患病的有20个样本.
（1）根据所给样本数据完成下面2×2列联表；
（2）请问能有多大把握认为药物有效？
| |
不得禽流感 |
得禽流感 |
总计 |
| 服药 |
|
|
|
| 不服药 |
|
|
|
| 总计 |
|
|
|
一项“过关游戏”规则规定：在第
关要抛掷一颗骰子次，如果这次抛掷所出现的点数的和大于
，则算过关，则某人连过前三关的概率是（ ）
A． |
B． |
C． |
D． |
设每个工作日甲、乙、丙、丁4人需使用某种设备的概率分别是0.6，0.5,0.5,0.4，各人是否使用设备相互独立，
（1）求同一工作日至少3人需使用设备的概率；
(2)实验室计划购买台设备供甲、乙、丙、丁使用，若要求"同一工作日需使用设备的人数大于
的概率小于0.1，求
的最小值.
一个袋子中装有6个红球和4个白球，假设袋子中的每一个球被摸到可能性是相等的。
（Ⅰ）从袋子中任意摸出3个球，求摸出的球均为白球的概率；
（Ⅱ）一次从袋子中任意摸出3个球，若其中红球的个数多于白球的个数，则称“摸球成功”（每次操作完成后将球放回），某人连续摸了3次，记“摸球成功”的次数为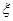
，求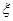的分布列和数学期望。
（本小题满分12分）某高中为了推进新课程改革，满足不同层次学生的需求，决定从高一年级开始，在每周的周一、周三、周五的课外活动期间同时开设数学、物理、化学、生物和信息技术辅导讲座，每位有兴趣的同学可以在期间的任何一天参加任何一门科目的辅导讲座，也可以放弃任何一门科目的辅导讲座。（规定：各科达到预先设定的人数时称为满座，否则称为不满座）统计数据表明，各学科讲座各天的满座的概率如下表：
根据上表：
（1）求数学辅导讲座在周一、周三、周五都不满座的概率；
（2）设周三各辅导讲座满座的科目数为
，求随机变量的分布列和数学期望．
在一次反恐演习中，我方三架武装直升机分别从不同方位对同一目标发动攻击（各发射一枚导弹），由于天气原因，三枚导弹命中目标的概率分别为0．9，0．9，0．8，若至少有两枚导弹命中目标方可将其摧毁，则目标被摧毁的概率为（ ）
| A．0．998 | B．0．046 | C．0．002 | D．0．954 |
为了解某班关注NBA（美国职业篮球）是否与性别有关，对某班48人进行了问卷调查得到如下的列联表：
| |
关注NBA |
不关注NBA |
合计 |
| 男生 |
|
6 |
|
| 女生 |
10 |
|
|
| 合计 |
|
|
48 |
已知在全班48人中随机抽取1人，抽到关注NBA的学生的概率为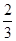
.
（1）请将上面的表补充完整（不用写计算过程），并判断是否有95%的把握认为关注NBA与性别有关？说明你的理由；
（2）设甲，乙是不关注NBA的6名男生中的两人，丙，丁，戊是关注NBA的10名女生中的3人，从这5人中选取2人进行调查，求：甲，乙至少有一人被选中的概率.
答题参考
| P（K2≥k） |
0.10 |
0.05 |
0.010 |
0.005 |
| k0 |
2.706 |
3.841 |
6.635 |
7.879 |
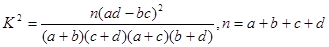
在乒乓球比赛中，甲与乙以“五局三胜”制进行比赛，根据以往比赛情况，甲在每一局胜乙的概率均为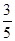 
．已知比赛中，乙先赢了第一局，求：
(Ⅰ)甲在这种情况下取胜的概率；
(Ⅱ)设比赛局数为X，求X的分布列及数学期望（均用分数作答）。
甲、乙两人独立地破译1个密码，他们能译出密码的概率分别为
和
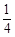，求
（1）恰有1人译出密码的概率；
（2）若达到译出密码的概率为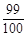
，至少需要多少乙这样的人．
一款击鼓小游戏的规则如下：每盘游戏都需要击鼓三次，每次击鼓要么出现一次音乐，要么不出现音乐；每盘游戏击鼓三次后，出现一次音乐获得10分，出现两次音乐获得20分，出现三次音乐获得100分，没有出现音乐则扣除200分（即获得-200分）.设每次击鼓出现音乐的概率为，且各次击鼓出现音乐相互独立.
（1）设每盘游戏获得的分数为，求
的分布列；
（2）玩三盘游戏，至少有一盘出现音乐的概率是多少？
（3）玩过这款游戏的许多人都发现，若干盘游戏后，与最初的分数相比，分数没有增加反而减少了.请运用概率统计的相关知识分析分数减少的原因.
已知某人每天早晨乘坐的某一班公共汽车的准时到站的概率为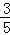
，则他在3天乘车中，此班车至少有2天准时到站的概率为（ ）
A． |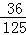
B． |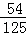
C． |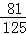
D． |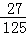
随机观测生产某种零件的某工厂
名工人的日加工零件数（单位：件），获得数据如下：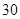
、
、
、
、
、
、
、、、
、
、
、
、、
、
、
、、
、、
、、
、
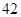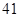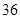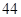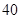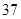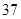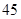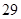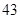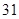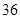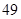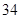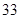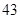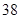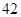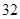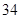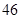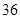、，根据上述数据得到样本的频率分布表如下：
| 分组 |
频数 |
频率 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|
 |
 |
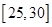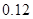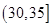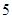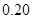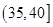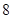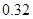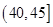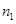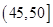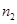（1）确定样本频率分布表中的值；
（2）根据上述频率分布表，画出样本频率分布直方图；
（3）根据样本频率分布直方图，求在该厂任取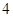
人，至少有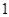
人的日加工零件数落在区间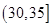的概率.
，则
________．
等于（ ）
粤公网安备 44130202000953号