河南省中原名校高三高考仿真模拟统一考试理科数学试卷
一只蚂蚁从正方体  ,的顶点A处出发,经正方体的表面,按最短路线爬行到达顶点
,的顶点A处出发,经正方体的表面,按最短路线爬行到达顶点  位置,则下列图形中可以表示正方体及蚂蚁最短爬行路线的正视图是
位置,则下列图形中可以表示正方体及蚂蚁最短爬行路线的正视图是
| A.①② | B.①③ | C.②④ | D.③④ |
等差数列  的前项n和为
的前项n和为  ,满足
,满足  ,则
,则  的值为
的值为
| A.2014 | B.-2014 | C.1 | D.0 |
已知双曲线  的一条渐近线方程是
的一条渐近线方程是  ,它的一个焦点在抛物线
,它的一个焦点在抛物线  的准线上,则双曲线线的方程为
的准线上,则双曲线线的方程为
A. |
B. |
C. |
D. |
设变量x,y满足约束条件  ,则目标函数z=
,则目标函数z= 的最大值为
的最大值为
| A.11 | B.10 | C.9. | D.13 |
已知函数 的导函数为
的导函数为  ,满足
,满足  ,且
,且 ,则
,则 的单调性情况为
的单调性情况为
A.先增后减 B单调递增 C.单调递减 D先减后增
已知函数  的值域为
的值域为  ,若关于x的不等式
,若关于x的不等式  的解集为
的解集为 ,则实数m的值为
,则实数m的值为
| A.25 | B.-25 | C.50 | D.-50 |
过原点的直线交双曲线  于P,Q两点,现将坐标平面沿直线y= -x折成直二面角,则折后PQ长度的最小值等于
于P,Q两点,现将坐标平面沿直线y= -x折成直二面角,则折后PQ长度的最小值等于
A. |
B.4 | C. |
D. |
已知  ABC的三个顶点在以O为球心的球面上,且
ABC的三个顶点在以O为球心的球面上,且  ,BC=1,AC=3,三棱锥O- ABC的体积为
,BC=1,AC=3,三棱锥O- ABC的体积为  ,则球O的表面积为__________。
,则球O的表面积为__________。
在△ABC中,己知  ,sinB= sinCcos
,sinB= sinCcos ,又△ABC的面积为6(Ⅰ)求△ABC的三边长;(Ⅱ)若D为BC边上的一点,且CD=1,求
,又△ABC的面积为6(Ⅰ)求△ABC的三边长;(Ⅱ)若D为BC边上的一点,且CD=1,求  .
.
在乒乓球比赛中,甲与乙以“五局三胜”制进行比赛,根据以往比赛情况,甲在每一局胜乙的概率均为 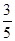 .已知比赛中,乙先赢了第一局,求:
.已知比赛中,乙先赢了第一局,求:
(Ⅰ)甲在这种情况下取胜的概率;
(Ⅱ)设比赛局数为X,求X的分布列及数学期望(均用分数作答)。
如图所示的几何体中,四边形ABCD是等腰梯形,AB//CD,  ,FC
,FC  平面ABCD, AE
平面ABCD, AE  BD,CB =CD=-CF.
BD,CB =CD=-CF.
(Ⅰ)求证:平面ABCD  平面AED;
平面AED;
(Ⅱ)直线AF与面BDF所成角的余弦值
已知椭圆  的离心率为
的离心率为  ,且过点
,且过点 

(Ⅰ)求椭圆的标准方程;
(Ⅱ)四边形ABCD的顶点在椭圆上,且对角线AC、BD过原点O,若  .
.
(i)求  的最值:
的最值:
(i i)求证:四边形ABCD的面积为定值.
设函数 
(Ⅰ)若 ,是否存在k和m,使得
,是否存在k和m,使得  ,
, ,若存在,求出k和m的值,若不存在,说明理由
,若存在,求出k和m的值,若不存在,说明理由
(Ⅱ)设  有两个零点
有两个零点  ,且
,且  成等差数列,
成等差数列,  是 G (x)的导函数,求证:
是 G (x)的导函数,求证: 
如图,四边形ABCD是边长为a的正方形,以D为圆心,DA为半径的圆弧与以BC为直径的半圆O交于点C、F,连接CF并延长交AB于点E.
(Ⅰ)求证:E是AB的中点。
(Ⅱ)求线段BF的长.
在直角坐标系中,以原点为极点,x轴的正半辐为极轴建立极坐标系,已知曲线 ,过点P(-2,-4)的直线
,过点P(-2,-4)的直线  的参数方程为:
的参数方程为: (t为参数),直线
(t为参数),直线 与曲线C相交于M,N两点.
与曲线C相交于M,N两点.
(Ⅰ)写出曲线C的直角坐标方程和直线 的普通方程;
的普通方程;
(Ⅱ)若 成等比数列,求a的值
成等比数列,求a的值
 ,则
,则 
 B.{1} C.[0,1] D.
B.{1} C.[0,1] D.
 ,则
,则





 服从正态分布
服从正态分布  若
若  ,则
,则  的值为
的值为

 为单位向量,若
为单位向量,若  满足
满足  ,则
,则  的最大值为
的最大值为

 的展开式中
的展开式中  的系数是_________(用数字作答)
的系数是_________(用数字作答) ,则tan 2a=_________.
,则tan 2a=_________. 的前n项和为
的前n项和为  ,满足
,满足  ,
,  的前n项和为
的前n项和为  ,则
,则 _________.
_________.
 的解集;
的解集; 恒成立,求实数a的取值范围
恒成立,求实数a的取值范围 粤公网安备 44130202000953号
粤公网安备 44130202000953号