高中数学正交试验设计方法试题

设随机变量X的分布列为P(X＝k)＝p^k(1－p)^1－k(k＝0.1,0＜p＜1)，则E(X)＝________.

在2008年北京奥运会羽毛球女单决赛中，中国运动员张宁以2：1力克排名世界第一的队友谢杏芳，蝉联奥运会女单冠军.羽毛球比赛按“三局二胜制”的规则进行（即先胜两局的选手获胜，比赛结束），且各局之间互不影响.根据两人以往的交战成绩分析，谢杏芳在前两局的比赛中每局获胜的概率是0.6，但张宁在前二局战成1：1的情况下，在第三局中凭借过硬的心理素质，获胜的概率为0.6.若张宁与谢杏芳下次在比赛上相遇.
（1）求张宁以2：1获胜的概率；
（2）求张宁失利的概率.

姚明比赛时罚球命中率为90%，则他在3次罚球中罚失1次的概率是      ．

乒乓球比赛规则规定，一局比赛，双方比分在10平前，一方连续发球2次后，对方再连续发球2次，依次轮换，每次发球，胜方得1分，负方得0分。设在甲、乙的比赛中，每次发球，发球1分的概率为0.6，各次发球的胜负结果相互独立。甲、乙的一局比赛中，甲先发球。
（I）求开球第4次发球时，甲、乙的比分为1比2的概率；
（II）求开始第5次发球时，甲得分领先的概率。

某班主任对全班50名学生进行了作业量多少的调查，数据如下表：

	认为作业多	认为作业不多	总数
喜欢玩电脑游戏	18	9	27
不喜欢玩电脑游戏	8	15	23
总数	26	24	50

根据表中数据得到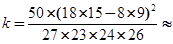5.059，因为p(K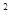≥5.024)=0.025,
则认为喜欢玩电脑游戏与认为作业量的多少有关系的把握大约为（ ）
(A)97.5%     (B) 95%       (C)90%        (D)无充分根据

(10分)有10件产品，其中有2件次品，从中随机抽取3件，求：
(1)其中恰有1件次品的概率；(2)至少有一件次品的概率、

甲、乙两人玩猜数字游戏，先由甲心中任想一个数字，记为a，再由乙猜甲刚才想的数字，把乙猜的数字记为b,且a,b {1，2，3，4},若|ab| 1,则称甲乙”心有灵犀”.现任意找两个人玩这个游戏,得出他们”心有灵犀”的概率为         （分式表示）

（本小题满分12分）已知A、B、C三个箱子中各装有2个完全相同的球，每个箱子里的球，有一个球标着号码1，另一个球标着号码2．现从A、B、C三个箱子中各摸出1个球．
（Ⅰ）若用数组中的分别表示从A、B、C三个箱子中摸出的球的号码，请写出数组的所有情形，并回答一共有多少种；
（Ⅱ）如果请您猜测摸出的这三个球的号码之和，猜中有奖．那么猜什么数获奖的可能性最大？请说明理由。

设随机变量X～B(2，p)，Y～B(3，p)，若P(X≥1)＝，则P(Y＝2)＝________.

某射手射击1次，击中目标的概率是0.9。她连续射击4次，且各次射击是否击中目标相互之间没有影响.有下列结论：
①他第3次击中目标的概率是0.9；
②他恰好击中目标3次的概率是；
③他至少击中目标1次的概率是；
④他击中目标2次的概率是0.81.
其中正确结论的序号是              （写出所有正确结论的序号）

设随机变量的概率分布列为

则（  ）

A．

B．

C．

D．

实验女排和育才女排两队进行比赛，在一局比赛中实验女排获胜的概率是2/3，没有平局．若采用三局两胜制，即先胜两局者获胜且比赛结束，则实验女排获胜的概率等于

A．

B．

C．

D．

甲、乙两人将参加某项测试，他们能达标的概率都是0.8，设随机变量为两人中能达标的人数，则的数学期望为        ．   

某射手射击1次，击中目标的概率是0.9，他连续射击4次，且各次射击是否击中目标相互之间没有影响，有下列结论：①他第3次击中目标的概率是0.9；②他恰好击中目标3次的概率是0.9³×0.1；③他至少击中目标1次的概率是1－0.1⁴.其中结论正确的是________．(写出所有正确结论的序号)

如图；现有一迷失方向的小青蛙在3处，它每跳动一次可以等机会地进入相邻的任意一格（如若它在5处，跳动一次，只能进入3处，若在3处，则跳动一次可以等机会进入l，2，4，5处），则它在第三次跳动后，进入5处的概率是

A．

B．

C．

D．