[2013·广东高考]设m,n是两条不同的直线,α,β是两个不同的平面.下列命题中正确的是( )
| A.若α⊥β,m⊂α,n⊂β,则m⊥n |
| B.若α∥β,m⊂α,n⊂β,则m∥n |
| C.若m⊥n,m⊂α,n⊂β,则α⊥β |
| D.若m⊥α,m∥n,n∥β,则α⊥β |
[2014·长春质检]如图,四棱锥P-ABCD的底面是一直角梯形,AB∥CD,BA⊥AD,CD=2AB,PA⊥底面ABCD,E为PC的中点,则BE与平面PAD的位置关系为________.
[2013·郑州模拟]设α,β,γ为三个不同的平面,m,n是两条不同的直线,在命题“α∩β=m,n⊂γ,且________,则m∥n”中的横线处填入下列三组条件中的一组,使该命题为真命题.
①α∥γ,n⊂β;②m∥γ,n∥β;③n∥β,m⊂γ.
可以填入的条件有( )
| A.①或② | B.②或③ |
| C.①或③ | D.①或②或③ |
[2014·福州质检]对于平面α和共面的直线m,n,下列命题是真命题的是( )
| A.若m,n与α所成的角相等,则m∥n |
| B.若m∥α,n∥α,则m∥n |
| C.若m⊥α,m⊥n,则n∥α |
| D.若m⊂α,n∥α,则m∥n |
[2013·安徽高考]在下列命题中,不是公理的是( )
| A.平行于同一个平面的两个平面相互平行 |
| B.过不在同一条直线上的三点,有且只有一个平面 |
| C.如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在此平面内 |
| D.如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线 |
已知三条不重合的直线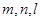 和两个不重合的平面
和两个不重合的平面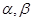 ,下列命题正确的是( )
,下列命题正确的是( )
A.若 , , ,则 ,则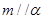 |
B.若 , ,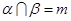 ,且 ,且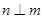 ,则 ,则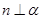 |
C.若 , , ,则 ,则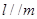 |
D.若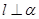 , , ,且 ,且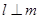 ,则 ,则 |
如图所示,PA⊥平面ABC,点C在以AB为直径的⊙O上,∠CBA=30°,PA=AB=2,点E为线段PB的中点,点M在弧AB上,且OM∥AC.
(1)求证:平面MOE∥平面PAC.
(2)求证:平面PAC⊥平面PCB.
(3)设二面角M—BP—C的大小为θ,求cos θ的值.
已知棱长为l的正方体 中,E,F,M分别是AB、AD、
中,E,F,M分别是AB、AD、 的中点,又P、Q分别在线段
的中点,又P、Q分别在线段 上,且
上,且 ,设面
,设面 面MPQ=
面MPQ= ,则下列结论中不成立的是( )
,则下列结论中不成立的是( )
A. 面ABCD B.
面ABCD B. AC
AC
C.面MEF与面MPQ不垂直 D.当x变化时, 不是定直线
不是定直线
设m,n是两条不同直线,α,β是两个不同的平面,下列命题正确的是( )
| A.m∥α,n∥β且α∥β,则m∥n |
| B.m⊥α,n⊥β且α⊥β,则m⊥n |
| C.m⊥α,n⊂β,m⊥n,则α⊥β |
| D.m⊂α,n⊂α,m∥β,n∥β,则α∥β |
下列命题中错误的是( )
| A.如果平面α⊥平面β,那么平面α内一定存在直线平行于平面β |
| B.如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面β |
| C.如果平面α⊥平面γ,平面β⊥平面γ,α∩β=l,那么l⊥平面γ |
| D.如果平面α⊥平面β,那么平面α内所有直线都垂直于平面β |
给定下列四个命题:
①若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行;
②若一个平面经过另一个平面的垂线,那么这两个平面相互垂直;
③垂直于同一直线的两条直线相互平行;
④若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直.
其中,为真命题的是( )
| A.①和② | B.②和③ | C.③和④ | D.②和④ |
平面α∥平面β的一个充分条件是( )
| A.存在一条直线a,a∥α,a∥β |
| B.存在一条直线a,a⊂α,a∥β |
| C.存在两条平行直线a,b,a⊂α,b⊂β,a∥β,b∥α |
| D.存在两条异面直线a,b,a⊂α,b⊂β,a∥β,b∥α |
“直线a∥直线β”是“直线a至少平行于平面β内的一条直线”的( )
| A.充要条件 | B.充分不必要条件 |
| C.必要不充分条件 | D.既不充分也不必要条件 |
已知直线a,b,平面α,β,则a∥α的一个充分条件是( )
| A.a⊥b,b⊥α | B.a∥β,β∥α |
| C.b⊂α,a∥b | D.a∥b,b∥α,a⊄α |