高中数学误差估计试题

统计某校1 000名学生的数学测试成绩，得到样本频率分布直方图如图所示，若满分为100分，规定不低于60分为及格，则及格率是（ ）

A．20%

B．25%

C．60%

D．80%

某中学为了解学生数学课程的学习情况，在3000名学生中随机抽取200名，并统计这200名学生的某次数学考试成绩，得到了样本的频率分布直方图（如下图）．根据频率分布直方图推测这3000名学生在该次数学考试中成绩小于60分的学生数是           ．
 

甲，乙两名运动员练习罚球，每人练习10组，每组罚球40个，命中个数的茎叶图如图，则甲，乙两命中个数的中位数分别为（ ）

A．23，19	B．24，18
C．22，20	D．23，20

为选拔选手参加“中国谜语大会”，某中学举行了一次“谜语大赛”活动．为了了解本次竞赛学生的成绩情况，从中抽取了部分学生的分数（得分取正整数，满分为分）作为样本（样本容量为）进行统计．按照的分组作出频率分布直方图，并作出样本分数的茎叶图（图中仅列出了得分在的数据）．

（1）求样本容量和频率分布直方图中的、的值；
（2）在选取的样本中，从竞赛成绩在分以上（含分）的学生中随机抽取名学生参加“中国谜语大会”，求所抽取的名学生中至少有一人得分在内的概率．

为了考察某校各班参加课外书法小组的人数，在全校随机抽取5个班级，把每个班级参加该小组的认为作为样本数据．已知样本平均数为7，样本方差为4，且样本数据互相不相同，则样本数据中的最大值为 ________．

在发生某公共卫生事件期间，有专业机构认为该事件在一段时间没有发生在规模群体感染的标志为“连续10天，每天新增疑似病例不超过7人”。根据过去10天甲、乙、丙、丁四地新增疑似病例数据，一定符合该标志的是

A．甲地：总体均值为3，中位数为4

B．乙地：总体均值为1，总体方差大于0

C．丙地：中位数为2，众数为3

D．丁地：总体均值为2，总体方差为3

若样本数据的标准差为，则数据的标准差为

A．

B．

C．

D．

某防疫站对学生进行身体健康调查，欲采用分层抽样的办法抽取样本．某中学共有学生名，抽取了一个容量为的样本，样本中男生人，则该中学共有女生（  ）

A．人

B．人

C．人

D．人

如图是某学校一名篮球运动员在场比赛中所得分数的茎叶图，则该运动员在这场比赛中得分的中位数为            ．

从某企业生产的某种产品中抽取100件，测量这些产品的一项质量指标值，由测量表得如下频数分布表：

质量指标值分组	[75，85）	[85，95）	[95，105）	[105，115）	[115，125）
频数	6	26	38	22	8

 
（1）在答题卡上作出这些数据的频率分布直方图 （用阴影表示）

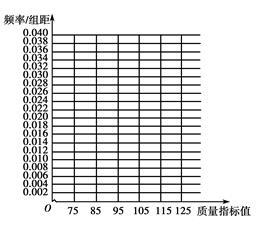
（2）估计这种产品质量指标值的平均数及中位数
（3）根据以上抽样调查数据，能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的80%”的规定？

某校高二甲、乙两学生统计了进入高中以来的十次统考成绩（如图），记甲、乙两学生成绩的中位数分别为，平均分分别为．则下列说法正确的是（   ）

A．	B．
C．	D．

样本的平均数为，样本的平均数为，则样本的平均数是（     ）

A．

B．

C．2

D．

某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛，他们取得的成绩（满分100分）的茎叶图如图，其中甲班学生的平均分是85，乙班学生成绩的中位数是83．则x+y的值为（ ）

A．7

B．8

C．9

D．10

从某校随机抽取100名学生，获得了他们一周课外阅读时间（单位：小时）的数据，整理得到数据分组及频数分布表和频率分布直方图：

（1）从该校随机选取一名学生，试估计这名学生该周课外阅读时间少于12小时的概率；
（2）求频率分布直方图中的a，b的值；
（3）假设同一组中的每个数据可用该组区间的中点值代替，试估计样本中的100名学生该周课外阅读时间的平均数在第几组（只需写出结论）

高二（8）班参加学校纪念“一二·九”学生爱国运动七十九周年合唱比赛的得分如茎叶图所示，根据比赛规则应去掉一个最高分和一个最低分，则最后成绩的中位数和平均数分别是（   ）

A．91．5和91．5

B．91．5和91

C．91和91．5

D．92和92