高中数学误差估计填空题

为选拔运动员参加比赛，测得7名选手的身高(单位：cm)分布茎叶图为记录的平均身高为177 cm，有一名候选人的身高记录不清楚，其末位数字记为x，那么x的值         .

交通管理部门为了解机动车驾驶员(简称驾驶员)对某新法规的知晓情况，对甲、乙、丙、丁四个社区做分层抽样调查．假设四个社区驾驶员的总人数为N，其中甲社区有驾驶员36人．若在甲、乙、丙、丁四个社区抽取驾驶员的人数分别为12，21，25，42，则这四个社区驾驶员的总人数N为     ．

某校为了解高一学生寒假期间的阅读情况，抽查并统计了100名同学的某一周阅读时间，绘制了频率分布直方图（如图所示），那么这100名学生中阅读时间在小时内的人数为_____．

随机抽取某中学位高三同学，调查他们春节期间购书费用（单位：元），获得数据的茎叶图如图，这位同学购书费用的中位数是__________．

从某项有400人参加的群众性运动的达标测试中，随机地抽取50人的成绩统计成如表，则400人的成绩的标准差的点估计值是        ．

分数	5	4	3	2	1
人数	5	15	20	5	5

某学校从高三年级共800名男生中随机抽取50名测量身高. 据测量被测学生身高全部介于155cm和195cm之间，将测量结果按如下方式分成八组：第一组、第二组、……、第八组. 按上述分组方式得到的频率分布直方图的一部分如图所示，估计这所学校高三年级全体男生身高180cm以上（含180cm）的人数为              .

如图是容量为200的样本的频率分布直方图，则样本数据落在[10,14]内的频数为   。

如下图所示，是某校高三年级文科60名同学参加谋科考试所得成绩（分数均为整数）整理后得出的频率分布直方图，根据该图这次考试文科60分以上的同学的人数为          .

为了了解学生的视力情况，随机抽查了一批学生的视力，将抽查结果绘制成频率分布直方图（如图所示）．若在[5.0，5.4]内的学生人数是2，则根据图中数据可得被样本数据在[3.8，4.2）内的人数是      ．

一个社会调查机构就某地居民的月收入调查了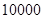人，并根据所得数据画了样本的频率分布直方图（如下图）．为了分析居民的收入与年龄、学历、职业等方面的关系，要从这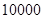人中再用分层抽样方法抽出人作进一步调查，则在（元）月收入段应抽出        人．

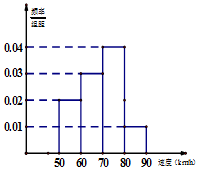
交通部门对某路段公路上行驶的汽车速度实施监控，从速度在的汽车中抽取150辆进行分析，得到数据的频率分布直方图如图所示，则速度在以下的汽车有        辆．

为了考察某校各班参加课外书法小组的人数，在全校随机抽取5个班级，把每个班级参加该小组的认为作为样本数据．已知样本平均数为7，样本方差为4，且样本数据互相不相同，则样本数据中的最大值为 ________．

一个总体分为A，B两层，用分层抽样方法从总体中抽取一个容量为10的样本，已知B层中每个个体被抽到的可能性都为，则总体中的个数为________．

某射击运动员在四次射击中分别打出了10，x，10，8环的成绩，已知这组数据的平均数为9，则这组数据的标准差是       ．

为了调查某厂工人生产某种产品的能力，随机抽查了20位工人某天生产该产品的数量，产品数量的分组区间为[45，55），[55，65），[65，75），[75，85），[85，95），由此得到频率分布直方图如图3，则这20名工人中一天生产该产品数量在[55，75）的人数是       ．