高中数学误差估计填空题

某校为了了解高三学生的身体状况，抽取了名女生,测量其体重.将所得的数据整理后，画出了如图所示的频率分布直方图，则所抽取的女生中体重在的人数是      

 

样本，，，，的方差为                      .

若一组样本数据，，，，的平均数为，则该组数据的方差       .

若样本的方差是2，则样本的方差是            

如图是某学校学生体重的频率分布直方图，已知图中从左到右的前个小组的频率之比为，第小组的频数为，则抽取的学生人数是            .

某学员在一次射击测试中射靶10次,命中环数如下:7, 8, 7, 9, 5, 4, 9, 10, 7, 4,则
(Ⅰ)平均命中环数为__________; 
(Ⅱ)命中环数的标准差为__________.

某种机器的使用年限和所支出的维修费用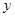(万元)有下表的统计资料：

	2	3	4	5	6
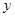	2.2	3.8	5.5	6.5	7.0

根据上表可得回归方程，据此模型估计，该种机器使用年限为10年时
维修费用约         万元（结果保留两位小数）．

下图茎叶图是甲、乙两人在5次综合测评中成绩，其中一个数字被污损，则甲的平均成绩超过乙的平均成绩的概率为         .

某行业从2013年开始实施绩效工资改革，为了解该行业职工工资收入情况，调查了lOOO名该行业的职工，并由所得数据画出了如图所示的频率分布直方图，由图可知中位数为:_____现要从这1000人中再用分层抽样的方法抽出100人作进一步调查，则月收入在[3500，4000)(元）内应抽出______人.

根据2012年初我国发布的《环境空气质量指数AQI技术规定（试行）》，AQI共分为六级：为优，为良，为轻度污染，为中度污染，为重度污染，300以上为严重污染．2013年5月1日出版的《A市早报》报道了A市2013年4月份中30天的AQI统计数据，下图是根据统计数据绘制的频率分布直方图. 根据图中的信息可以得出A市该月环境空气质量优良的总天数为           ．

甲、乙两名运动员在8场篮球比赛中得分的数据统计 如右图，则甲乙两人发挥较为稳定的是_____.

右图是某高三学生进入高中三年来第次到次的数学考试成绩茎叶图, 根据茎叶图计算数据的中位数为         .

根据某固定测速点测得的某时段内过往的100辆机动车的行驶速度(单位：km/h)绘制的频率分布直方图如右图所示．该路段限速标志牌提示机动车辆正常行驶速度为60 km/h~120 km/h，则该时段内非正常行驶的机动车辆数为     ．

给出下列5种说法：①在频率分布直方图中，众数左边和右边的直方图的面积相等；②标准差越小，样本数据的波动也越小；③回归分析就是研究两个相关事件的独立性；④在回归分析中，预报变量是由解释变量和随机误差共同确定的；⑤相关指数是用来刻画回归效果的，的值越大，说明残差平方和越小，回归模型的拟合效果越好. 其中说法正确的是____________（请将正确说法的序号写在横线上）.

根据《中华人民共和国道路交通安全法》规定：车辆驾驶员血液酒精浓度在20～80 /100（不含80）之间，属于酒后驾车；血液酒精浓度在80/100（含80）以上时，属醉酒驾车．据《法制晚报》报道，2013年1月1日至1月7日，全国查处酒后驾车和醉酒驾车共38800人，如图是对这38800人酒后驾车血液中酒精含量进行检测所得结果的频率分布直方图，则属于醉酒驾车的人数约为______．