[江苏]2014届江苏南京市、盐城市高三第一次模拟考试理数学试卷
在平面直角坐标系 中,若中心在坐标原点上的双曲线的一条准线方程为
中,若中心在坐标原点上的双曲线的一条准线方程为 ,且它的一个顶点与抛物线
,且它的一个顶点与抛物线 的焦点重合,则该双曲线的渐进线方程为 .
的焦点重合,则该双曲线的渐进线方程为 .
设函数 ,则“
,则“ 为奇函数”是“
为奇函数”是“ ”的 条件.(选填“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”)
”的 条件.(选填“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”)
如图,现要在边长为 的正方形
的正方形 内建一个交通“环岛”.正方形的四个顶点为圆心在四个角分别建半径为
内建一个交通“环岛”.正方形的四个顶点为圆心在四个角分别建半径为 (
( 不小于
不小于 )的扇形花坛,以正方形的中心为圆心建一个半径为
)的扇形花坛,以正方形的中心为圆心建一个半径为 的圆形草地.为了保证道路畅通,岛口宽不小于
的圆形草地.为了保证道路畅通,岛口宽不小于 ,绕岛行驶的路宽均不小于
,绕岛行驶的路宽均不小于 .
.
(1)求 的取值范围;(运算中
的取值范围;(运算中 取
取 )
)
(2)若中间草地的造价为 元
元 ,四个花坛的造价为
,四个花坛的造价为 元
元 ,其余区域的造价为
,其余区域的造价为 元
元 ,当
,当 取何值时,可使“环岛”的整体造价最低?
取何值时,可使“环岛”的整体造价最低?
在平面直角坐标系 中,已知过点
中,已知过点 的椭圆
的椭圆 :
: 的右焦点为
的右焦点为 ,过焦点
,过焦点 且与
且与 轴不重合的直线与椭圆
轴不重合的直线与椭圆 交于
交于 ,
, 两点,点
两点,点 关于坐标原点的对称点为
关于坐标原点的对称点为 ,直线
,直线 ,
, 分别交椭圆
分别交椭圆 的右准线
的右准线 于
于 ,
, 两点.
两点.
(1)求椭圆 的标准方程;
的标准方程;
(2)若点 的坐标为
的坐标为 ,试求直线
,试求直线 的方程;
的方程;
(3)记 ,
, 两点的纵坐标分别为
两点的纵坐标分别为 ,
, ,试问
,试问 是否为定值?若是,请求出该定值;若不是,请说明理由.
是否为定值?若是,请求出该定值;若不是,请说明理由.
已知函数 ,
, .
.
(1)若 ,则
,则 ,
, 满足什么条件时,曲线
满足什么条件时,曲线 与
与 在
在 处总有相同的切线?
处总有相同的切线?
(2)当 时,求函数
时,求函数 的单调减区间;
的单调减区间;
(3)当 时,若
时,若 对任意的
对任意的 恒成立,求
恒成立,求 的取值的集合.
的取值的集合.
设等差数列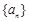 的前
的前 项和为
项和为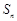 ,已知
,已知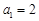 ,
, .
.
(1)求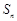 ;
;
(2)若从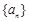 中抽取一个公比为
中抽取一个公比为 的等比数列
的等比数列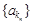 ,其中
,其中 ,且
,且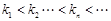 ,
,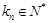 .
.
①当 取最小值时,求
取最小值时,求 的通项公式;
的通项公式;
②若关于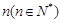 的不等式
的不等式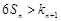 有解,试求
有解,试求 的值.
的值.
在极坐标系中,圆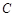 的方程为
的方程为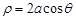 ,以极点为坐标原点,极轴为
,以极点为坐标原点,极轴为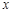 轴的正半轴建立平面直角坐标系,直线
轴的正半轴建立平面直角坐标系,直线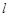 的参数方程为
的参数方程为 (
( 为参数),若直线
为参数),若直线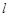 与圆
与圆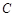 相切,求实数
相切,求实数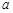 的值.
的值.
已知点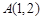 在抛物线
在抛物线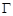 :
: 上.
上.
(1)若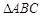 的三个顶点都在抛物线
的三个顶点都在抛物线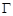 上,记三边
上,记三边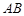 ,
, ,
,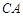 所在直线的斜率分别为
所在直线的斜率分别为 ,
,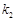 ,
, ,求
,求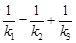 的值;
的值;
(2)若四边形 的四个顶点都在抛物线
的四个顶点都在抛物线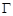 上,记四边
上,记四边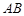 ,
, ,
, ,
,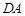 所在直线的斜率分别为
所在直线的斜率分别为 ,
,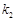 ,
, ,
,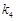 ,求
,求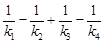 的值.
的值.
 ,集合
,集合 ,则
,则 .
. (
( 为虚数单位)为纯虚数,则实数
为虚数单位)为纯虚数,则实数 .
. 人中随机选派
人中随机选派 人参加某项活动,则甲被选中的概率为 .
人参加某项活动,则甲被选中的概率为 . 的值为 .
的值为 .
 ,
, ,
, ,
, ,
, 的平均数为
的平均数为 ,则该组数据的方差
,则该组数据的方差 .
. 中,若点
中,若点 到直线
到直线 的距离为
的距离为 ,且点
,且点 在不等式
在不等式 表示的平面区域内,则
表示的平面区域内,则 .
. 中,底面
中,底面 是边长为
是边长为 的菱形,
的菱形, ,侧棱
,侧棱 底面
底面 ,
, 为
为 的中点,则四面体
的中点,则四面体 的体积为 .
的体积为 .
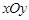 中,若圆
中,若圆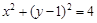 上存在
上存在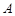 ,
,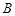 两点关于点
两点关于点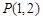 成中心对称,则直线
成中心对称,则直线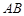 的方程为 .
的方程为 .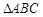 中,
中,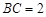 ,
,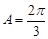 ,则
,则 的最小值为 .
的最小值为 .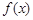 是定义在
是定义在 上的偶函数,且在区间
上的偶函数,且在区间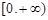 上是单调增函数.如果实数
上是单调增函数.如果实数 满足
满足 时,那么
时,那么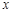 的不等式
的不等式 对任意的正实数
对任意的正实数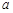 的取值范围是 .
的取值范围是 . 的首项为
的首项为 ,公比为
,公比为 ,其前
,其前 项和为
项和为 ,若
,若 对
对 恒成立,则
恒成立,则 的最小值为
的最小值为  中,角
中,角 ,
, ,
, 所对的边分别是
所对的边分别是 ,
, ,
, ,已知
,已知 ,
, .
. ,求
,求 ,求
,求 中,
中, ,
, 分别为
分别为 ,
, 的中点.
的中点.
 平面
平面 ;
; 平面
平面 .
. ,
,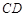 是半径为
是半径为 的圆
的圆 的两条弦,它们相交于
的两条弦,它们相交于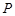 ,若
,若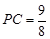 ,
,  ,求
,求 的长.
的长.
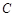 :
: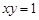 ,若矩阵
,若矩阵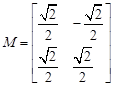 对应的变换将曲线
对应的变换将曲线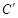 ,求曲线
,求曲线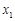 ,
, ,
, 为正实数,若
为正实数,若 ,求证:
,求证: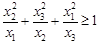 .
.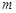 是给定的正整数,有序数组(
是给定的正整数,有序数组(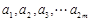 )中
)中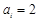 或
或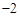
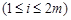 .
. ,
, ,都有
,都有 ”的有序数组(
”的有序数组(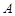 ;
;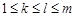 ,
,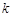 ,
,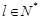 ,都有
,都有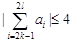 成立,求满足“存在
成立,求满足“存在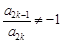 ”的有序数组(
”的有序数组( .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号