[吉林]2013届吉林省长春市高中毕业班第四次调研测试理科数学试卷
关于复数 ,下列说法中正确的是( )
,下列说法中正确的是( )
A.在复平面内复数 对应的点在第一象限 对应的点在第一象限 |
B.复数 的共轭复数 的共轭复数 |
C.若复数  为纯虚数,则 为纯虚数,则 |
D.设 为复数 为复数 的实部和虚部,则点 的实部和虚部,则点 在以原点为圆心,半径为1的圆上 在以原点为圆心,半径为1的圆上 |
设函数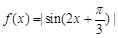 ,则下列关于函数
,则下列关于函数 的说法中正确的是( )
的说法中正确的是( )
A. 是偶函数 是偶函数 |
B. 最小正周期为π 最小正周期为π |
C. 图象关于点 图象关于点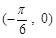 对称 对称 |
D. 在区间 在区间 上是增函数 上是增函数 |
如图,平面内有三个向量 ,其中
,其中 与
与 的夹角为
的夹角为 ,
, 与
与 的夹角为
的夹角为 ,且
,且 ,若
,若 ,则( )
,则( )
A. |
B. |
C. |
D. |

若数列 满足规律:
满足规律: ,则称数列
,则称数列 为余弦数列,现将1,2,3,4,5排列成一个余弦数列的排法种数为( )
为余弦数列,现将1,2,3,4,5排列成一个余弦数列的排法种数为( )
| A.12 | B.14 | C.16 | D.18 |
已知双曲线
 以及双曲线
以及双曲线
 的渐近线将第一象限三等分,则双曲线
的渐近线将第一象限三等分,则双曲线 的离心率为( )
的离心率为( )
A.2或 |
B. 或 或 |
C.2或 |
D. 或 或 |
已知空间4个球,它们的半径分别为2, 2, 3, 3,每个球都与其他三个球外切,另有一个小球与这4个球都外切,则这个小球的半径为( )
A. |
B. |
C. |
D. |
给出下列5种说法:①在频率分布直方图中,众数左边和右边的直方图的面积相等;②标准差越小,样本数据的波动也越小;③回归分析就是研究两个相关事件的独立性;④在回归分析中,预报变量是由解释变量和随机误差共同确定的;⑤相关指数 是用来刻画回归效果的,
是用来刻画回归效果的, 的值越大,说明残差平方和越小,回归模型的拟合效果越好. 其中说法正确的是____________(请将正确说法的序号写在横线上).
的值越大,说明残差平方和越小,回归模型的拟合效果越好. 其中说法正确的是____________(请将正确说法的序号写在横线上).
数列 满足
满足
 ,且
,且 .
.
(1) 求数列 的通项公式;
的通项公式;
(2) 令 ,当数列
,当数列 为递增数列时,求正实数
为递增数列时,求正实数 的取值范围.
的取值范围.
为了研究玉米品种对产量的影响,某农科院对一块试验田种植的一批玉米共10000 株的生长情况进行研究,现采用分层抽样方法抽取50株作为样本,统计结果如下:
| |
高茎 |
矮茎 |
合计 |
| 圆粒 |
11 |
19 |
30 |
| 皱粒 |
13 |
7 |
20 |
| 合计 |
24 |
26 |
50 |
(1) 现采用分层抽样的方法,从这个样本中取出10株玉米,再从这10株玉米中随机选出3株,求选到的3株之中既有圆粒玉米又有皱粒玉米的概率;
(2) 根据对玉米生长情况作出的统计,是否能在犯错误的概率不超过0.050的前提下认为玉米的圆粒与玉米的高茎有关?(下面的临界值表和公式可供参考:
| P(K2≥k) |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
| k |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
 ,其中
,其中 )
)
如图,平面四边形 的4个顶点都在球
的4个顶点都在球 的表面上,
的表面上, 为球
为球 的直径,
的直径, 为球面上一点,且
为球面上一点,且 平面
平面  ,
, ,点
,点 为
为 的中点.
的中点.
(1) 证明:平面 平面
平面 ;
;
(2) 求平面 与平面
与平面 所成锐二面角的余弦值.
所成锐二面角的余弦值.
已知 、
、 是椭圆
是椭圆
 的左、右焦点,且离心率
的左、右焦点,且离心率 ,点
,点 为椭圆上的一个动点,
为椭圆上的一个动点, 的内切圆面积的最大值为
的内切圆面积的最大值为 .
.
(1) 求椭圆的方程;
(2) 若 是椭圆上不重合的四个点,满足向量
是椭圆上不重合的四个点,满足向量 与
与 共线,
共线, 与
与 共
共
线,且 ,求
,求 的取值范围.
的取值范围.
已知函数 .
.
(1) 当 时,求函数
时,求函数 的单调区间;
的单调区间;
(2) 当 时,函数
时,函数 图象上的点都在
图象上的点都在 所表示的平面区域内,求实数
所表示的平面区域内,求实数 的取值范围.
的取值范围.
(3) 求证: ,(其中
,(其中 ,
, 是自然对数的底).
是自然对数的底).
如图, 是
是 的切线,
的切线, 过圆心
过圆心 ,
,  为
为 的直径,
的直径, 与
与 相交于
相交于 、
、 两点,连结
两点,连结 、
、 . (1) 求证:
. (1) 求证: ;
;
(2) 求证: .
.
在极坐标系内,已知曲线 的方程为
的方程为 ,以极点为原点,极轴方向为
,以极点为原点,极轴方向为 正半轴方向,利用相同单位长度建立平面直角坐标系,曲线
正半轴方向,利用相同单位长度建立平面直角坐标系,曲线 的参数方程为
的参数方程为 (
( 为参数).
为参数).
(1) 求曲线 的直角坐标方程以及曲线
的直角坐标方程以及曲线 的普通方程;
的普通方程;
(2) 设点 为曲线
为曲线 上的动点,过点
上的动点,过点 作曲线
作曲线 的两条切线,求这两条切线所成角余弦值的取值范围.
的两条切线,求这两条切线所成角余弦值的取值范围.
 ,则
,则 为( )
为( )







 的前
的前 项和为
项和为 ,且满足
,且满足 ,则公比
,则公比 =( )
=( )


 值为( )
值为( )
 的展开式中常数项为( )
的展开式中常数项为( )
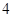
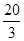

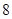

 满足约束条件
满足约束条件 ,若目标函数
,若目标函数 的最大值为6,则
的最大值为6,则 ______.
______. 的图像和其在点
的图像和其在点 处的切线与
处的切线与 轴所围成区域的面积为________.
轴所围成区域的面积为________.
 满足
满足 ,
, ,则不等式
,则不等式 的解集为______.
的解集为______. ,
, .
. ;
; ,且
,且 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号