.下图是某次民族运动会上,七位评委为某民族舞蹈节目打出分数的茎叶图。去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
7  9
9
8 4 4 6 4 7
9 3
| A.84,4.84 | B.84,1.6 | C.85,1.6 | D.85,4 |
某科研部门现有男技术员45人,女技术员15人,为研发某新产品的需要,科研部门按照分层抽样的方法组建了一个由四人组成的新产品研发小组.
(1)求每一个技术员被抽到的概率及该新产品研发小组中男、女技术员的人数;
(2)一年后研发小组决定选两名研发的技术员对该项研发产品进行检验,方法是先从研发小组中选一人进行检验,该技术员检验结束后,再从研发小组内剩下的三名技术员中选一人进行检验,若两名技术员检验得到的数据如下:
| 第一次被抽到进行检验的技术员 |
58 |
53 |
87 |
62 |
78 |
70 |
82 |
| 第二次被抽到进行检验的技术员 |
64 |
61 |
78 |
66 |
74 |
71 |
76 |
① 求先后被选出的两名技术员中恰有一名女技术员的概率;
② 请问哪位技术员检验更稳定?并说明理由.
图1是根据某班学生在一次数学考试
中的成绩画出的频率分布直方图,若80
分以上为优秀,根据图形信息可知:
这次考试的优秀率为
A. |
B. |
C.  |
D. |

对某种花卉的开放花期追踪调查,调查情况如下:
| 花期(天) |
11~13 |
14~16 |
17~19 |
20~22 |
个 数 数 |
20 |
40 |
30 |
10 |
则这种卉的平均花期为___天.
、一组数据的平均数是2.8,方差是3.6,若将这组数据中的每一个数据都加上60,得到一组新数据,则所得新数据的平均数和方差分别是 ,
某校数学教研组为了解学生学习数学的情况,采用分层抽样的方法从高一600人、高二680人、高三720人中,抽取50人进行问卷调查,则高一、高二、高三抽取的人数分别是
| A.15,16,19 | B.15,17,18 | C.14,17,19 | D.15,16,20 |
下图是样本容量为200的频率分布直方图. 根据样 本的频率分布直方图估计,样本数据落在 内的频数为 ;数据落在
内的频数为 ;数据落在 内的概率约为 .
内的概率约为 .

某校组织一次篮球投篮测试,已知甲同学每次投篮的命中率均为1/2。
(1)若规定每投进1球得2分,甲同学投篮4次,求总得分X的概率分布和数学期望。
(2)假设连续3次投篮未中或累计7次投篮未中,则停止投篮测试,问:甲同学恰好投篮10次,被停 止投篮测试的概率是多少?
止投篮测试的概率是多少?
为了解某校教师使用多媒体进行教学的情况,采用简单随机抽样的
方法,从该校200名授课教师中抽取20名教师,调查了他们上学期
使用多媒体进行教学的次数,结果用茎叶图表示如右:据此可估计
该校上学期200名教师中,使用多媒体进行教学次数在 内的
内的
人数为 
某工厂对一批产品长度进行抽样检测. 如图,是根据抽样检测后的产品长度(单位:厘米)数据绘制的频率分布直方图,其中产品 长度的范围是[34,44],样本数据分组为[34,36),[36,38),[38,40),[40,42),[42,44]. 已知样本中产品长度小于38厘米的个数是36,则样本中净重大于或等于36厘米并且小于42厘米的产品的个数是
长度的范围是[34,44],样本数据分组为[34,36),[36,38),[38,40),[40,42),[42,44]. 已知样本中产品长度小于38厘米的个数是36,则样本中净重大于或等于36厘米并且小于42厘米的产品的个数是 
| A.45 | B.60 | C.75 | D.90 |
(本小题满分12分)
某校高三数学竞赛初赛考试后,对考生成绩进行统计(考生成绩均不低于90分,满分150分),将成绩按如下方式分成六 组,第一组
组,第一组 、第二组
、第二组 …第六组
…第六组 . 如图为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人.
. 如图为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人.
(Ⅰ)请补充完整频率分布直方图,并估
计这组数据的平均数M;
(Ⅱ)现根据初赛成绩从第四组和第六组
中任意选2人,记他们的成绩分别
为 . 若
. 若 ,则称此二
,则称此二
人为“黄金帮扶组”,试求选出的二
人错误!链接无效。的概率 ;
;
(Ⅲ)以此样本的频率当作概率,现随机在这组样本中选出的3名学生,求成绩不低于
120分的人数 分布列及期望
分布列及期望 .
.
(本小题满分12分)
某中学对高二甲、乙两个同类班级进行“加强‘语文阅读理解’训练对提高‘数学应用题’得分率作用”的试验,其中甲班为试验班(加强语文阅读理解训练),乙班为对比班(常规教学,无额外训练),在试验前的测试中,甲、乙两班学生在数学应用题上的得分率基本一致,试验结束后,统计几次数学应用题测试的平均成绩(均取整数)如下表所示:
| |
60分以下 |
61-70分 |
71-80分 |
81-90分 |
91-100分 |
| 甲班(人数) |
3 |
6 |
11 |
18 |
12 |
| 乙班(人数) |
4 |
8 |
13 |
15 |
10 |
现规定平均成绩在80分以上(不含80分)的为优秀.
(Ⅰ)试分别估计两个班级的优秀率;
(Ⅱ)由以上统计数据填写下面2×2列联表,并问是否有75%的把握认为“加强‘语文阅读理解’训练对提高‘数学应用题’得分率”有帮助.
| |
优秀人数 |
非优秀人数 |
合计 |
| 甲班 |
|
|
|
| 乙班 |
|
|
|
| 合计 |
|
|
|
甲、乙两名运动员的5次测试成绩如下图所示设 分别表示甲、乙两名运动员测试成绩的标准差,
分别表示甲、乙两名运动员测试成绩的标准差, 分别表示甲、乙两名运动员测试成绩的平均数,则有 ( )
分别表示甲、乙两名运动员测试成绩的平均数,则有 ( )
A. , , |
B. , ,  |
C. , ,  |
D. , ,  |
| 甲 |
|
乙 |
| 3 5 |
1 |
4  6 6 |
| 6 6 0 |
2 |
1 4 5 |

(本小题满分12分)
某校高三数学竞赛初赛考试后,对考生成绩进行统计(考生成绩均不低于90分,满分150分),将成绩按如下方式分成六组,第一组 、第二组
、第二组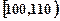 …第六组
…第六组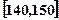 . 如图为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人.
. 如图为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人.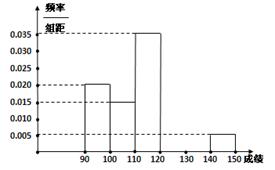
(Ⅰ)请补充完整频率分布直方图,并估
计这组数据的平均数M;
(Ⅱ)现根据初赛成绩从第四组和第六组中任意选2人,记他们的成绩分别为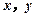 . 若
. 若 ,则称此二人为“黄金帮扶组”,试求选出的二人为“黄金帮扶组”的概率
,则称此二人为“黄金帮扶组”,试求选出的二人为“黄金帮扶组”的概率 ;
;
(Ⅲ)以此样本的频率当作概率,现随机在这组样本中选出的3名学生,求成绩不低于120分的人数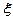 分布列及期望.
分布列及期望.