河南省郑州市高三毕业班第二次模拟考试数学理卷
设函数y= 的定义域为M,集合N={y|y=
的定义域为M,集合N={y|y= ,x∈R},则M∩N=
,x∈R},则M∩N=
A. |
B.N | C.[1,+∞) | D.M |
已知△ABC中,sinA :sinB :sinC=1 :1 : ,则此三角形的最大内角的度数是
,则此三角形的最大内角的度数是
| A.60° | B.90° | C.120° | D.135° |
设a、b是两条不同的直线, 、β是两个不同的平面,则下列四个命题:
、β是两个不同的平面,则下列四个命题:
①若a⊥b,a⊥ ,b
,b
 ,则b∥
,则b∥ ; ②若a∥
; ②若a∥ ,a⊥
,a⊥ ,则
,则 ⊥
⊥ ;
;
③若a⊥ ,
, ⊥
⊥ ,则a∥
,则a∥ 或a
或a
 ; ④若a⊥b,a⊥
; ④若a⊥b,a⊥ ,b⊥
,b⊥ ,则
,则 ⊥
⊥
其中正确命题的个数为
| A.1 | B.2 | C.3 | D.4 |
已知随机变量ξ服从正态分布N(1, ),P(ξ≤4)=0.84,则P(ξ≤-2)=
),P(ξ≤4)=0.84,则P(ξ≤-2)=
| A.0.16 | B.0.32 | C.0.68 | D.0.84 |
要得到函数y=cos2x的图象,只需将函数y=sin(2x+ )的图象沿x轴
)的图象沿x轴
A.向左平移 个单位 个单位 |
B.向左平移 个单位 个单位 |
C.向右平移 个单位 个单位 |
D.向右平移 个单位 个单位 |
下面的程序框图给出了计算数列{ }的前8项和S的算法,算法执行完毕后,输出的S为
}的前8项和S的算法,算法执行完毕后,输出的S为
| A.8 | B.63 | C.92 | D.129 |
.5位同学站成一排准备照相的时候,有两位老师碰巧
路过,同学们强烈要求与老师合影留念,如果5位同
学顺序一定,那么两位老师与同学们站成一排照相的
站法总数为
| A.6 | B.20 | C.30 | D.42 |
设f(x)= 则不等式f(x)<2的解集为
则不等式f(x)<2的解集为
A.( ,+∞) ,+∞) |
B.(-∞,1)∪[2, ) ) |
C.(1,2]∪( ,+∞) ,+∞) |
D.(1, ) ) |
设双曲线4 (t≠0)的两条渐近线与直线x=
(t≠0)的两条渐近线与直线x= 围成的三角形区域(包含边界)为D,P(x,y)为D内的一个动点,则目标函数z=
围成的三角形区域(包含边界)为D,P(x,y)为D内的一个动点,则目标函数z= x-y的最小值为
x-y的最小值为
| A.-2 | B.- |
C.0 | D.- |
设抛物线 =4y的焦点为F,经过点P(1,4)的直线l与抛物线相交于A、B两点,且点P恰为AB的中点,则|
=4y的焦点为F,经过点P(1,4)的直线l与抛物线相交于A、B两点,且点P恰为AB的中点,则|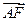 |+|
|+|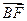 |=________________.
|=________________.
设f(x)是R上的奇函数,且f(-1)=0,当x>0时,( +1)
+1) (x)-2xf(x)<0,则不等式f(x)>0的解集为______________.
(x)-2xf(x)<0,则不等式f(x)>0的解集为______________.
(本小题满分12分)
已知数列{ }的前n项和
}的前n项和 =2-
=2- ,数列{
,数列{ }满足b1=1, b3+b7=18,且
}满足b1=1, b3+b7=18,且 +
+ =2
=2 (n≥2).
(n≥2).
(Ⅰ)求数列{ }和{
}和{ }的通项公式;
}的通项公式;
(Ⅱ)若 =
= ,求数列{
,求数列{ }的前n项和
}的前n项和 .
.
(本小题满分12分)
某中学对高二甲、乙两个同类班级进行“加强‘语文阅读理解’训练对提高‘数学应用题’得分率作用”的试验,其中甲班为试验班(加强语文阅读理解训练),乙班为对比班(常规教学,无额外训练),在试验前的测试中,甲、乙两班学生在数学应用题上的得分率基本一致,试验结束后,统计几次数学应用题测试的平均成绩(均取整数)如下表所示:
| |
60分以下 |
61-70分 |
71-80分 |
81-90分 |
91-100分 |
| 甲班(人数) |
3 |
6 |
11 |
18 |
12 |
| 乙班(人数) |
4 |
8 |
13 |
15 |
10 |
现规定平均成绩在80分以上(不含80分)的为优秀.
(Ⅰ)试分别估计两个班级的优秀率;
(Ⅱ)由以上统计数据填写下面2×2列联表,并问是否有75%的把握认为“加强‘语文阅读理解’训练对提高‘数学应用题’得分率”有帮助.
| |
优秀人数 |
非优秀人数 |
合计 |
| 甲班 |
|
|
|
| 乙班 |
|
|
|
| 合计 |
|
|
|
(本小题满分12分)
如图,四棱柱ABCD-A1B1C1D1中,A1D⊥平面ABCD,底面ABCD是边长为1的正方形,侧棱AA1=2.
(Ⅰ)求三棱锥C-A1B1C1的体积V;
(Ⅱ)求直线BD1与平面ADB1所成角的正弦值;
(Ⅲ)若棱AA1上存在一点P,使得 =λ
=λ ,
,
当二面角A-B1C1-P的大小为30°时,求实
数λ的值.
((本小题满分12分)
在平面直角坐标系xOy中,点P(x,y)为动点,已知点A( ,0),B(-
,0),B(- ,0),直线PA与PB的斜率之积为定值-
,0),直线PA与PB的斜率之积为定值- .
.
(Ⅰ)求动点P的轨迹E的方程;
(Ⅱ)若F(1,0),过点F的直线l交轨迹E于M、N两点,以MN为对角线的正方形的第三个顶点恰在y轴上,求直线l的方程.
((本小题满分12分)
已知x> ,函数f(x)=
,函数f(x)= ,h(x)=2e lnx(e为自然常数).
,h(x)=2e lnx(e为自然常数).
(Ⅰ)求证:f(x)≥h(x);
(Ⅱ)若f(x)≥h(x)且g(x)≤h(x)恒成立,则称函数h(x)的图象为函数f(x),g(x)的“边界”.已知函数g(x)=-4 +px+q(p,q∈R),试判断“函数f(x),g(x)以函数h(x)的图象为边界”和“函数f(x),g(x)的图象有且仅有一个公共点”这两个条件能否同时成立?若能同时成立,请求出实数p、q的值;若不能同时成立,请说明理由.
+px+q(p,q∈R),试判断“函数f(x),g(x)以函数h(x)的图象为边界”和“函数f(x),g(x)的图象有且仅有一个公共点”这两个条件能否同时成立?若能同时成立,请求出实数p、q的值;若不能同时成立,请说明理由.
选修4—1:(本小题满分10分)几何证明选讲
如图,在△ABC中,∠C为钝角,点E,
H分别是边AB上的点,点K和M分别
是边AC和BC上的点,且AH=AC,EB
=BC,AE=AK,BH=BM.
(Ⅰ)求证:E、H、M、K四点共圆;
(Ⅱ)若KE=EH,CE=3,求线段KM的
长.




 ,|a|=
,|a|= ,则a在b方向上的投影为
,则a在b方向上的投影为


 ,则这个正方体的棱长是
,则这个正方体的棱长是



 +mi(i为虚数单位)为实数,则实数m=_______________.
+mi(i为虚数单位)为实数,则实数m=_______________.
 ,
, ,求ac+bd的最大值.
,求ac+bd的最大值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号