((本小题满分12分)
在平面直角坐标系xOy中,点P(x,y)为动点,已知点A(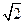 ,0),B(-
,0),B(-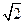 ,0),直线PA与PB的斜率之积为定值-
,0),直线PA与PB的斜率之积为定值-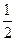 .
.
(Ⅰ)求动点P的轨迹E的方程;
(Ⅱ)若F(1,0),过点F的直线l交轨迹E于M、N两点,以MN为对角线的正方形的第三个顶点恰在y轴上,求直线l的方程.
推荐套卷
((本小题满分12分)
在平面直角坐标系xOy中,点P(x,y)为动点,已知点A(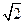 ,0),B(-
,0),B(-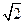 ,0),直线PA与PB的斜率之积为定值-
,0),直线PA与PB的斜率之积为定值-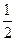 .
.
(Ⅰ)求动点P的轨迹E的方程;
(Ⅱ)若F(1,0),过点F的直线l交轨迹E于M、N两点,以MN为对角线的正方形的第三个顶点恰在y轴上,求直线l的方程.