（（本小题满分12分）
已知x>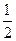
，函数f（x）＝
，h（x）＝2e lnx（e为自然常数）．
（Ⅰ）求证：f（x）≥h（x）；
（Ⅱ）若f（x）≥h（x）且g（x）≤h（x）恒成立，则称函数h（x）的图象为函数f（x），g（x）的“边界”．已知函数g（x）＝－4＋px＋q（p，q∈R），试判断“函数f（x），g（x）以函数h（x）的图象为边界”和“函数f（x），g（x）的图象有且仅有一个公共点”这两个条件能否同时成立?若能同时成立，请求出实数p、q的值；若不能同时成立，请说明理由．
相关试题
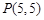，且和圆C：
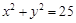相交，截得弦长为
，求l的方程.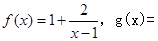
f(2x)
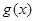在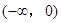
上为减函数。
上的最小值.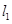
：
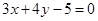与直线
：
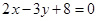的交点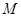
，且满足下列条件的直线方程
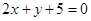平行 ； 如图，椭圆
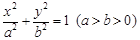经过点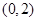
，其左、右顶点分别是
、
，左、右焦点分别是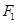
、
，
（异于、）是椭圆上的动点，连接
交直线
于
、
两点,若
成等比数列.
（Ⅰ）求此椭圆的离心率；
（Ⅱ）求证:以线段
为直径的圆过点.
的圆形（
为圆心）铁皮上截取一块矩形材料
，其中点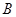
在圆弧上，点
在两半径上，现将此矩形材料卷成一个以
为母线的圆柱形罐子的侧面（不计剪裁和拼接损耗），设
与矩形材料的边
的夹角为
，圆柱的体积为
.
相关知识点
推荐套卷
粤公网安备 44130202000953号