如图，半径为30
的圆形（
为圆心）铁皮上截取一块矩形材料
，其中点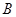
在圆弧上，点
在两半径上，现将此矩形材料卷成一个以
为母线的圆柱形罐子的侧面（不计剪裁和拼接损耗），设
与矩形材料的边
的夹角为
，圆柱的体积为
.
（Ⅰ）求关于的函数关系式？
（Ⅱ）求圆柱形罐子体积的最大值.
相关试题
的对边分别为
；
求
=
-1.
的取值范围;
，
-
恒成立，求
的取值范围。
.
的单调区间；
="1" ,
为整数,且当
0时,
，求
的前n项和
（其中
为常数）,且
="4" 
=8
.
；
的前
项和
.
=
的部分图象如图所示。
=
－
的单调递增区间。推荐套卷
如图，半径为30的圆形（为圆心）铁皮上截取一块矩形材料，其中点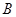在圆弧上，点在两半径上，现将此矩形材料卷成一个以为母线的圆柱形罐子的侧面（不计剪裁和拼接损耗），设与矩形材料的边的夹角为，圆柱的体积为.
（Ⅰ）求关于的函数关系式？
（Ⅱ）求圆柱形罐子体积的最大值.
粤公网安备 44130202000953号