高中数学误差估计试题

成都市为“市中学生知识竞赛”进行选拔性测试，且规定：成绩大于或等于90分的有参赛资格，90分以下（不包括90分）的则被淘汰。若现有500人参加测试，学生成绩的频率分布直方图如下：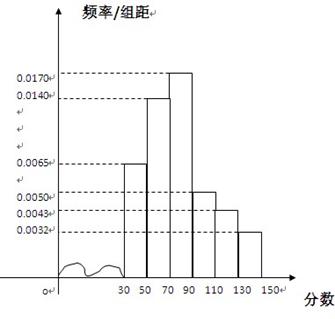

（I）求获得参赛资格的人数；
（II）根据频率直方图，估算这500名学生测试的平均成绩；
（III）若知识竞赛分初赛和复赛，在初赛中每人最多有3次选题答题的机会，累计答对2题或答错2题即终止，答对2题者方可参加复赛，已知参赛者甲答对每一个问题的概率都相同，并且相互之间没有影响，已知他连续两次答错的概率为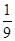，求甲通过初赛的概率.

有一个容量为66的样本，数据的分组及各组的频数如下：
[11．5,15．5)　2　[15．5,19．5)　 4　[19．5,23．5)　9
[23．5,27．5)　18　[27．5,31．5)　11　[31．5,35．5)　12
[35．5,39．5)　7　[39．5,43．5)　3
根据样本的概率分布估计，大于或等于31．5的数据约占(　　)

A．

B．

C．

D．

在数学趣味知识培训活动中，甲、乙两名学生的6次培训成绩如下茎叶图所示：

(Ⅰ)从甲、乙两人中选择1人参加数学趣味知识竞赛，你会选哪位？请运用统计学的知识说明理由；
(II)从乙的6次培训成绩中随机选择2个，试求选到123分的概率．

某校100名学生期中考试语文成绩的频率分布直方图如图所示，其中成绩分组区间是：[50,60），[60,70），[70,80），[80,90），[90,100]．

（1）求图中a的值；
（2）根据频率分布直方图，估计这100名学生语文成绩的平均分；
（3）若这100名学生语文成绩某些分数段的人数（x）与数学成绩相应分数段的人数（y）之比如下表所示，
求数学成绩在[50,90）之外的人数．

分数段	[50,60）	[60, 70）	[70,80）	[80,90）
x∶y	1∶1	2∶1	3∶4	4∶5

 

某学校100名学生期中考试语文成绩的频率分布直方图如下右图所示，其中成绩分组区间是：，，，，。
求图中a的值；
根据频率分布直方图，估计这100名学生语文成绩的平均分；

若这100名学生语文成绩某些分数段的人数与数学成绩相应分数段的人数
之比如下表所示，求数学成绩在之外的人数。

分数段
x：y	1：1	2：1	3：4	4：5

 

某学校为了解该校600名男生的百米成绩（单位：s），随机选择了50名学生进行调查，
下图是这50名学生百米成绩的频率分布直方图。根据样本的频率分布，估计这600名学生中成绩在（单位：s）内的人数大约是       .

（本小题满分12分）我市为积极相应《全民健身条例》大力开展学生体育活动，如图是委托
调查机构在市区的两所学校校、校中分别随机抽取了名高二年级的学生当月体育锻炼时间的茎
叶图（单位：小时）

（1）根据茎叶图，分别写将两所学校学生当月体育锻炼 时间的众数、中位数和平均数填入下表；

	校	校
众数
中位数
平均数

 
（2）根据茎叶图，求校学生的月体育锻炼时间的方差；
（3）若学生月体育锻炼的时间低于小时，就说明该生体育锻炼时间严重不足．根据茎叶图估计、
两所学校的学生体育锻炼严重不足的频率．

国家环境标准制定的空气质量指数与空气质量等级对应关系如下表：

由全国重点城市环境监测网获得2月份某五天甲城市和乙城市的空气质量指数数据用茎叶图表示如图：

（Ⅰ）试根据上面的统计数据，判断甲、乙两个城市的空气质量指数的方差的大小关系（只需写出结果）；
（Ⅱ）试根据上面的统计数据，估计甲城市某一天空气质量等级为2级良的概率；
（Ⅲ）分别从甲城市和乙城市的统计数据中任取一个，试求这两个城市空气质量等级相同的概率．
（注：s²=[（x₁﹣）²+（x₂﹣）²+…+（x_n﹣）²]，其中为数据x₁，x₂，…，x_n的平均数．）

2015年五一节”期间，高速公路车辆“较多，交警部门通过路面监控装置抽样调查某一山区路段汽车行驶速度，采用的方法是：按到达监控点先后顺序，每隔50辆抽取一辆，总共抽取120辆，分别记下其行车速度，将行车速度（km/h）分成七段[60，65），[65，70），[70，75），[75，80），[80，85），[85，90），[90，95）后得到如图所示的频率分布直方图，据图解答下列问题：

（1）求a的值，并说明交警部门采用的是什么抽样方法？
（2）若该路段的车速达到或超过90km/h即视为超速行驶，试根据样本估计该路段车辆超速行驶的概率；
（3）求这120辆车行驶速度的众数和中位数的估计值（精确到0．1）。

某校从高二年级学生中随机抽取60名学生，将其期中考试的政治成绩（均为整数）分成六段：，，…， 后得到如下频率分布直方图．

（Ⅰ）求分数在内的频率； 
（Ⅱ）根据频率分布直方图，估计该校高二年级学生期中考试政治成绩的平均分；
（Ⅲ）用分层抽样的方法在80分以上（含80分）的学生中抽取一个容量为6的样本，将该样本看成一个总体，从中任意选取2人，求其中恰有1人的分数．不低于90分的概率．

某校从参加高一年级期中考试的学生中随机抽出60名学生，将其数学成绩（均为整数）分成六段[40,50)，[50,60)，．．．，[90,100]后得到如图所示的部分频率分布直方图．观察图形的信息，回答下列问题：

（1）求分数在[70,80)内的频率，并补全这个频率分布直方图，统计方法中，同一组数据常用该组区间的中点值作为代表，据此估计本次考试的平均分；
（2）若从60名学生中随机抽取2人，抽到的学生成绩在[40,60)记0分，在[60,80)记1分，在[80,100]记2分，用表示抽取结束后的总记分，求的分布列和数学期望．

对某班学生是爱好体育还是爱好文娱进行调查，根据调查得到的数据，所绘制的二维条形图如图．
（1）根据图中的数据，填好2×2列表，并计算在多大的程度上可以认为性别与是否爱好体育有关系：
（2）若已从男生中选出3人，女生中选出2人，从这5人中选出2人担任活动的协调人，求选出的两人性别相同的概率．

	男	女	总计
爱好体育
爱好文娱
总  计

参考数据：

	0．5	0．4	0．25	0．15	0．10	0．05	0．025	0．010	0．005	0．001
	0．455	0．708	1．323	2．072	2．706	3．841	5．024	6．635	7．879	10．828

参考公式：

《中华人民共和国道路交通安全法》规定：车辆驾驶员血液酒精浓度在20～80mg/100ml（不含80）之间，属于酒后驾车；在80mg/100ml（含80）以上时，属于醉酒驾车．某市公安局交通管理部门在某路段的一次拦查行动中，依法检查了300辆机动车，查处酒后驾车和醉酒驾车的驾驶员共20人，检测结果如下表：

（1）绘制出检测数据的频率分布直方图（在图中用实线画出矩形框即可）；
（2）求检测数据中醉酒驾驶的频率，并估计检测数据中酒精含量的众数、平均数．

将容量为n的样本中的数据分成6组，绘制频率分布直方图. 若第一组至第六组数据的频率之比为2:3:4:6: 4:1，且前三组数据的频数之和等于36，则n等于   ．

某高校在2011年的自主招生考试成绩中随机抽取100名学生的笔试成绩，按成绩分组：第1组[75，80)，第2组[80，85)，第3组[85，90)，第4组[90，95)，第5组
[95，100]得到的频率分布直方图如图所示．
(1)分别求第3，4，5组的频率；
(2)若该校决定在笔试成绩高的第3，4，5组中用分层抽样抽取6名学生进入第二轮面试，求第3，4，5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下，学校决定在这6名学生中随机抽取2名学生接受甲考官的面试，求第4组至少有一名学生被甲考官面试的概率．